Понятие числовой последовательности и ее предела

Если каждому натуральному числу 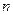по некоторому закону поставлено в соответствие определенное действительное число, то говорят, что задана числовая последовательность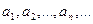

Числа 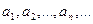называются членами последовательности; 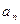называют общим членом последовательности.

Пример последовательности:

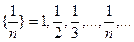
Введем понятие предела числовой последовательности. Число А называется пределом числовой последовательности 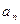, если для любого как угодно малого положительного числа 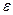существует номер N такой, что все члены последовательности 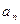с номерами n>N удовлетворяют следующему неравенству:

.

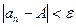Обозначения: 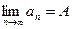или .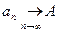

Определение. Последовательность 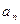называется сходящейся, если она имеет (конечный) предел, и расходящейся, если она предела не имеет.

Теорема (критерий Коши, необходимое и достаточное условие сходимости последовательности). Для сходимости последовательности 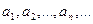необходимо и достаточно, чтобы для любого числа 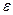существовал номер N такой, что для всех m, n>N выполнялось неравенство .

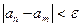Последовательность 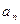, удовлетворяющая условию Коши, называется фундаментальной.

Теорема (единственной предела последовательности). Последовательность не может иметь двух различных пределов.