Электрохимия

Следующий раздел относится к решению задач повышенной сложности и предназначен для дополнительных заданий с соответствующим коэффициентом сложности бально-рейтинговой системы.

Электрохимические методы широко в современных промышленных технологиях. Для управления качеством получаемых материалов и для проектирования промышленных аппаратов необходимо знание природы электродных процессов, распределения электрических и концентрационных полей и влияния на них различных факторов.

Имеются многочисленные примеры, когда возможности экспериментальных методов для определения необходимых характеристик ограничены. В этом случае компьютерное моделирование представляется необходимым дополнительным методом исследования. Кроме того, даже в простых случаях моделирование электродных процессов позволяет получать данные, недоступные электрохимическим методам или связанные с трудоемкими и длительными вычислениями. Рассмотрим кратко основы электрохимии.

Из курса химии известно, что передача вещества в электролитах осуществляется путем диффузии, миграции и конвекции с учетом материальных балансов и баланса заряда. Для описания уравнения потока была предложена система линейных уравнений:

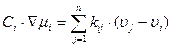(101)

где μ_i - электрохимический потенциал i-ого типа ионов; k_ij – коэффициент трения; υ_i – скорости ионов i-ого типа.

Однако, в общем случае, установить связь между коэффициентами трудно. При электрохимическом моделировании принимается ряд допущений: - коэффициенты диффузии не зависят от концентрации вещества, что справедливо при низких концентрациях изучаемого иона, - коэффициенты активности постоянны при низких концентрациях, - конвективная составляющая транспорта вещества отсутствует в пределах толщины диффузионного слоя, - миграционная составляющая также не учитывается.

В основе любого электрохимического процесса лежит закон Фарадея, согласно которому,количество выделившегося на катоде или растворившегося с анода вещества прямо пропорционально количеству электричества, прошедшего через электрохимическую ячейку и обратно пропорционально электрохимическому эквиваленту:

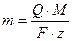(102)

где M/z – электрохимический эквивалент, в котором M – молярная масса, г/моль, z- число электронов, участвующих в реакции; Q – количество пропущенного через электроды электричества 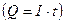, Кл; m – масса выделившегося или растворившегося вещества, г; F – число Фарадея, которое составляет 96493 Кл·г/эквивалент.

Таким образом, процесс электролиза – это процесс выделения или растворения на электродах – разноименно заряженных проводниках – вещества при прохождении через них постоянного электрического тока. На катоде – отрицательно заряженном электроде – разряжаются положительно заряженные частицы – катионы:

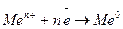
Или

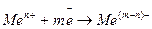(103)

На аноде – положительно заряженном электроде – разряжаются отрицательные ионы – анионы:

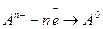или

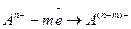(104)

Как видно, при электролизе не обязательно образуются на электродах новые вещества, возможен и перезаряд ионов электролита.

Для электролиза важны такие характеристики как электропроводность раствора, сопротивление электролита, подвижность ионов, напряжение разложения, нормальный окислительно-восстановительный потенциал Все эти параметры характерны для каждого вещества, но зависят от содержания этого вещества в растворе, т.е. от концентрации.

Энергия, необходимая для разряда ионов на электродах, зависит от разности потенциалов между раствором и электродом. Зависимость равновесного потенциала от концентрации ионов в растворе выражается формулой Нернста:

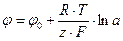(105)

где φ – потенциал электрода, В;

φ₀ – стандартный электродный потенциал, В;

R – универсальная газовая постоянная, Дж/(моль*К);

T – абсолютная температура, К;

z – число электронов, участвующих в электродном процессе;

F – число Фарадея, Кл/моль (Кл*г-экв);

А – активность ионов.

Для разбавленных растворов активность можно заменить концентрацией. При 25^оС уравнение Нернста принимает следующий вид:

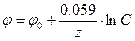(106)

Таким образом, стандартный потенциал φ₀ – это потенциал, отвечающий концентрации ионов в растворе, равной одному г*ион/л. Чем активней металл, т.е. чем легче он отдает электроны, тем более отрицательным будет его стандартный потенциал.

При потенциале, вычисляемом по формуле Нернста, разряд иона может протекать при силе тока, близкой к нулю. На практике процесс протекает в неравновесном состоянии и поэтому для разряда иона необходимо прилагать более отрицательный (по сравнению с уравнением (107)) потенциал. Разница между равновесным и неравновесным потенциалами называется перенапря­жением, а само отклонение потенциала от равновесного является поляризацией. Последняя может быть обусловлена следующими причинами:

- изменение концентрации ионов в двойном слое из-за недостаточной скорости подвода ионов, так называемая, концентрационная поляризация;

- образование продуктов электрохимической реакции, отличных от материала электрода, что меняет природу поверхности электрода – химическая поляризация;

- высокой энергией активации, что замедляет саму электрохимическую реакцию – электрохимическая поляри­зация, что равносильно перенапряжению.

Рассмотрим некоторые конкретные примеры исполь­зования электрохимических методов исследования.

Потенциометрическое титрование

Потенциометрия – это непосредственное определение концентрации ионов в растворе, исходя из эксперимен­тально измеренной величины электродного потенциала. Существует прямая линейная зависимость между потенциалом индикаторного электрода – электрода, реагирующего на изменение концентрации иона в растворе - и логарифмом концентрации потенциалопределяющего иона в титруемой системе. Другими словами, определяется концентрация иона в растворе. Очень важен выбор индикаторного электрода. Электрохимический метод отличается большей точностью по сравнению с другими методами анализа.

Рассмотрим пример определения концентрации ионов водорода, т.е. pH раствора. Запишем уравнение Нернста применительно к данному случаю:

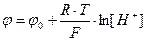(107)

В этом методе важен не сам электродный потенциал, а его изменение:

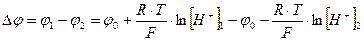(108)

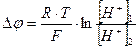(109)

В растворе всегда присутствуют ионы водорода и гидроксид-ионы. При титровании раствора в систему постепенно в малых количествах и небольшой скоростью вводится вещество, связывающее ион по известной, хорошо изученной реакции, концентрацию которого необходимо определить. Следовательно, концентрация, в данном случае, водорода в растворе постоянно уменьшается.

Расчет интегралов на компьютере.

Развитие электронно-вычислительных средств позволяет решать прикладные задачи, в частности, задачи моделирования, с большей точностью. Зачастую развитие компьютерного моделирования, кроме отсутствия законов изменения моделируемого объекта или процесса, было ограничено трудоемкостью расчетов. Даже достаточно изученный процесс или объект смоделировать и обсчитать не всегда просто.

Чаще всего сложности возникают при определении производных и расчете интегралов функций. В случае естественнонаучных дисциплин обычно применяют определенные интегралы сложных функций. В период отсутствия электронно-вычислительных приборов математика использовала приближенные или численные методы расчета производных функций и интегралов. Все эти методы основаны на разбиении изучаемого отрезка параметра функции на конечное число шагов.

Современный этап развития науки и техники, в частности, информатики, позволяет решать прикладные задачи без использования приближенных методов вычислений.

Согласно определению [1], неопределенным интегралом от функции 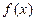или от ее дифференциального выражения 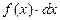называется общее выражение для всех первообразных данной непрерывной функции 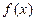и обозначается символом 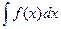. Под определенным интегралом 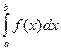от данной непрерывной функции 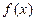на данном отрезке 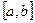понимается соответствующее приращение ее первообразной: 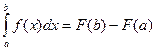. При этом число 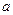– нижний предел интегрирования, число 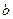– верхний предел интегрирования, 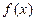- подынтегральная функция. Геометрический смысл заключается в том, что определенный интеграл от непрерывной неотрицательной функции при 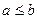равен площади соответствующей криволинейной трапеции.

Рассмотрим произвольную функцию f(x) на промежутке [x₁,x_n]. Интеграл функции f(x) на этом промежутке есть площадь криволинейной трапеции, ограниченной по оси у самой функцией 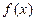, а по оси х – координатами х1 и xn.

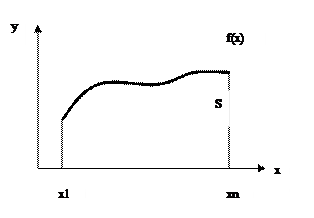
Рис.6 Произвольная функция у(х).

Площадь криволинейной трапеции можно представить как сумму некоторого количества элементарных трапеций с основанием ∆х. Тогда, обозначив искомый интеграл как S, можно записать, что 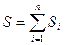. Расчет суммы методами программирования осуществляется с использованием любого оператора цикла: цикла с параметром или циклов с условием. Выглядит это следующим образом:

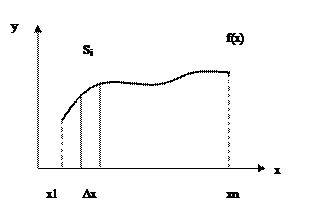
Рис. 7 Графическая интерпретация интеграла.

N:=10; S:=0; dx:=(xn-x1)/n;

Fori:=1 tondo

Begin

A:=dx*random(100):

S:=S+a;

End;

Данная запись означает, что к первоначальной переменной S=0 на каждом шаге цикла с параметром суммируется некоторая переменная а.

Либо:

X:=x1; s:=0;

Readln(xn); readln(dx);

While x < xn do begin

X:=x+dx;

Y:=x*x-5;

S:=S+y*dx

End;

Или, для случая массива данных:

Readln(x[1]); readln(xn); readln(dx);

S[0]:=0; i:=1;

While x[i] < xn do begin

Y[i]:=sqr(x[i]);

S[i]:=s[i-1]+y[i]*dx;

I:=i+1;

X[i]:=x[i-1]+dx’

End;

В данных примерах условие работы цикла записано не по количеству шагов вычисления, а по условию достижения пределов переменной (параметра). Второй и третий вариант расчета площади криволинейной трапеции предпочтительней, т.к., во-первых, можно не указывать количество итераций вычислений и, следовательно, нет нужды заранее оговаривать количество шагов, и, во-вторых, позволяет выполнять расчеты с заданной погрешностью. Например,

Readln(x[0], eps, xn, dx);

I:=0; y[i]:= exp(x[i])/sqrt(x[i]);

Repeat

I:=i+1;

X[i]:=x[i-1]+dx;

Y[i]:=exp(x[i])/sqrt(x[i]);

Until abs(y[i]-y[i-1]) < eps;

Вернемся к интегралам. Если уменьшать основание элементарной трапеции ∆х до значений, близких к нулю, то можно постепенно перейти к дифференциалу dx.

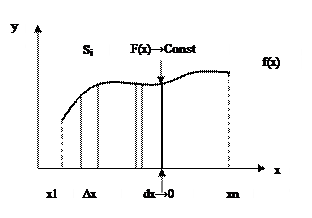
Рис. 8 Пример постепенного уменьшения дискретного интервала ∆x до бесконечно малого dx.

При 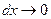функция f(x) в каждой точке кривой стремится к постоянной величине. Следовательно, функция может быть разбита на бесконечное множество констант. От дискретной величины суммы 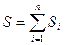можно перейти к непрерывной сумме величин, в данном случае, элементарных площадей .

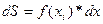Простейший пример расчета определенного интеграла для конкретной задачи рассматривается в практической (2 части) методического пособия.

Используемая литература

1. Луценко В.И., Финякин Л.Н. Математическое моделирование химико-технологических процессов на аналоговых вычислительных машинах. Лабораторный практикум. М., Химия, 1984.

2. Могилев А.В., Пак Н.И., Хеннер Е.К. Информатика. М., Академия, 2000.

3. Могилев А.В., Пак Н.И., Хеннер Е.К. Практикум по информатике. М., Академия, 2001.

4. Пак Н.И. Компьютерное моделирование в примерах и задачах. Красноярск, 1994.

5. Тарасевич Ю. Ю. Математическое и компьютерное моделирование. –М.: Едиториал УРСС. 2001. – 144 с.

6. В.А.Кудрявцев, Б.П.Демидович. Краткий курс высшей математики. Издание седьмое, исправленное. Москва, «Наука». Главная редакция физико-математической литературы. 1989. 656 с.

7. Компьютеры, модели, вычислительный эксперимент. Введение в информатику с позиций математического моделирования. Под ред. Самарского А.И. М., Наука, 1988.

8. Дьяконов В.П. Справочник по алгоритмам и программам на языке Бейсик для персональных ЭВМ. М., Наука, 1987.

9. Системы информационной поддержки регионального развития. КНЦ РАН, Апатиты, 1998.

10. Гольбрайх З.Е., Маслов Е.И., Сборник задач и упражнений по химии. М., Высшая школа, 1997.

11. Ерыгин Д.П., Шишкин Е.А. Методика решения задач по химии. Уч. пособие для пед. инст., М., Просвещение, 1989.

12. Горстко А.Б. Познакомьтесь с математическим моделированием. М., Знание, 1991.

13. К. Эберт, Х. Эдерер Компьютеры. Применение в химии. Пер. с нем., под ред. Н.С.Зефирова. М., Мир, 1988.

14. Кононова З.А. Расчет интегралов на ЭВМ. Проблемы непрерывного образования: проектирование, управление, функционирование: Материалы международной научно-практической конференции. (19-20 мая 2008г.; Липецк): В 3 ч. – Липецк: ЛГПУ, 2008. Ч.III.- с. 135.