Логарифмически нормальное распределение нашло широкое применение в вопросах техники, биологии, экономики и теории надежности. Его успешно применяют дня описания наработки до отказа подшипников, электронных ламп и других изделий.
Неотрицательная случайная величина распределена логарифмически нормально, если ее логарифм распределен нормально. Плотность распределения для различных значений σ приведена на рис. 3.
Плотность распределения описывается зависимостью
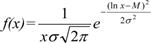 (18)
(18)
где М и σ — параметры, оцениваемые по результатам п испытаний до отказа;
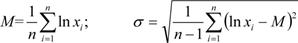 (19)
(19)
Для логарифмически нормального закона распределения функция надежности выглядит так:
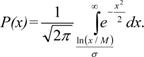 (20)
(20)
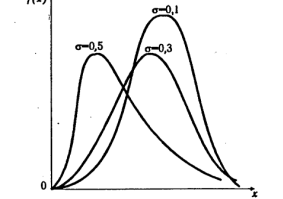
Рис. 3. Плотность логарифмически нормального распределения.
Вероятность безотказной работы можно определить по таблицам для нормального распределения (см. табл.П.1 приложения) в зависимости от значения квантили
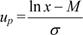
Математическое ожидание наработки до отказа
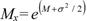 (21)
(21)
Среднее квадратическое отклонение и коэффициент вариации соответственно равны:
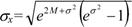 (22)
(22)
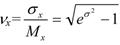 (23)
(23)
При vx ≤. 0,3 полагают, что vx = σ, при этом ошибка не более 1%.
Часто применяют запись зависимостей для логарифмически нормального закона в десятичных логарифмах. В соответствии с этим законом плотность распределения
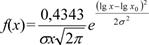 (24)
(24)
Оценки параметров lg x0 и σ определяют по результатам испытаний:
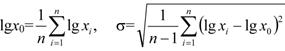 (25)
(25)
Математическое ожидание Мx, среднее квадратическое отклонение σ x и коэффициент вариации vx наработки до отказа соответственно равны:
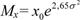 (26)
(26)
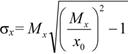 (27)
(27)
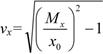 (28)
(28)
Пример 6. Определить вероятность безотказной работы редуктора в течение t =103 ч, если ресурс распределен логарифмически нормально с параметрами lg t0 = 3,6, σ =0,3.
Р е ш е н и е. Найдем значение квантили и по ней определим вероятность безотказной работы (табл. П.1 приложения):
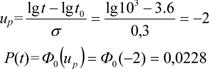
Ответ: P (t)=0,0228.
 2015-01-21
2015-01-21 8548
8548
