1 этап. Выбор формы связи между признаками
На основании рисунка 6.1 предположим, что связь между стоимостью собственных оборотных средств и средним размером активов описывается линейным уравнением регрессии 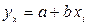 .
.
2 этап. Построение уравнения связи
Для расчета коэффициентов a, b линейного уравнения регрессии построим таблицу вспомогательных расчетов 6.3.
Сами параметры уравнения регрессии можно определить двумя способами:
1 способ. С использованием готовых формул (по данным последней строки таблицы 6.3):
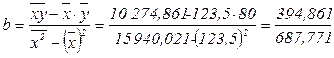 = 0,574 млн.руб./ млн. руб.;
= 0,574 млн.руб./ млн. руб.;
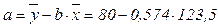 =9,097 млн. руб.
=9,097 млн. руб.
2 способ. С использованием системы нормальных уравнений для линейной формы связи между факторным признаком  и результативным признаком
и результативным признаком 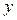 :
:
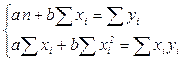
Таблица 6.3
Таблица вспомогательных расчетов для построения уравнения регрессии
| № предприятия | № п/п | Стоимость СОС, млн. руб. | Размер балансовой прибыли, млн. руб. | Вспомогательные расчеты | ||
| Выровненные значения по уравнению прямой | ||||||
| i | (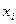 ) )
| (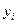 ) )
| xi ∙ yi | 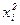
| 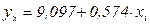
| |
| 62,0 | 50,0 | 3 100,00 | 3 844,00 | 44,7 | ||
| 63,5 | 50,0 | 3 175,00 | 4 032,25 | 45,6 | ||
| 88,4 | 59,0 | 5 215,60 | 7 814,56 | 59,8 | ||
| 91,2 | 51,0 | 4 651,20 | 8 317,44 | 61,5 | ||
| 91,2 | 59,5 | 5 426,40 | 8 317,44 | 61,5 | ||
| 94,7 | 59,5 | 5 634,65 | 8 968,09 | 63,5 | ||
| 101,5 | 66,0 | 6 699,00 | 10 302,25 | 67,4 | ||
| 104,9 | 59,0 | 6 189,10 | 11 004,01 | 69,3 | ||
| 105,1 | 71,0 | 7 462,10 | 11 046,01 | 69,4 | ||
| 105,1 | 71,0 | 7 462,10 | 11 046,01 | 69,4 | ||
| 115,7 | 72,0 | 8 330,40 | 13 386,49 | 75,5 | ||
| 116,3 | 82,5 | 9 594,75 | 13 525,69 | 75,9 | ||
| 116,5 | 82,5 | 9 611,25 | 13 572,25 | 76,0 | ||
| 116,9 | 76,0 | 8 884,40 | 13 665,61 | 76,2 | ||
| 116,9 | 78,5 | 9 176,65 | 13 665,61 | 76,2 | ||
| 117,1 | 75,0 | 8 782,50 | 13 712,41 | 76,3 | ||
| 118,1 | 74,0 | 8 739,40 | 13 947,61 | 76,9 | ||
| 118,1 | 74,0 | 8 739,40 | 13 947,61 | 76,9 | ||
| 118,1 | 76,0 | 8 975,60 | 13 947,61 | 76,9 | ||
| 118,3 | 76,0 | 8 990,80 | 13 994,89 | 77,0 | ||
| 119,3 | 76,0 | 9 066,80 | 14 232,49 | 77,6 | ||
| 119,3 | 76,0 | 9 066,80 | 14 232,49 | 77,6 | ||
| 119,3 | 83,5 | 9 961,55 | 14 232,49 | 77,6 | ||
| 123,0 | 83,5 | 10 270,50 | 15 129,00 | 79,7 | ||
| 127,2 | 82,5 | 10 494,00 | 16 179,84 | 82,1 | ||
| 127,2 | 85,0 | 10 812,00 | 16 179,84 | 82,1 | ||
| 127,6 | 85,0 | 10 846,00 | 16 281,76 | 82,4 | ||
| 137,6 | 89,5 | 12 315,20 | 18 933,76 | 88,1 | ||
| 138,6 | 89,5 | 12 404,70 | 19 209,96 | 88,7 | ||
| 138,6 | 89,5 | 12 404,70 | 19 209,96 | 88,7 | ||
| 138,6 | 89,5 | 12 404,70 | 19 209,96 | 88,7 | ||
| 146,3 | 95,0 | 13 898,50 | 21 403,69 | 93,1 | ||
| 146,3 | 95,5 | 13 971,65 | 21 403,69 | 93,1 | ||
| 153,1 | 92,5 | 14 161,75 | 23 439,61 | 97,0 | ||
| 163,0 | 101,5 | 16 544,50 | 26 569,00 | 102,7 | ||
| 163,0 | 106,0 | 17 278,00 | 26 569,00 | 102,7 | ||
| 163,2 | 100,0 | 16 320,00 | 26 634,24 | 102,8 | ||
| 163,2 | 101,5 | 16 564,80 | 26 634,24 | 102,8 | ||
| 173,0 | 106,0 | 18 338,00 | 29 929,00 | 108,4 | ||
| 173,0 | 110,0 | 19 030,00 | 29 929,00 | 108,4 | ||
| Сумма | 4 940 | 3 200 | 410 994,45 | 637 600,86 | 3 200 | |
| Среднее | 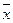 =123,5 =123,5
| 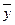 =80 =80
| 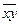 =10 274,861 =10 274,861
| 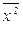 =15 940,021 =15 940,021
| 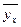 =80 =80
|
На основании данных таблицы 6.3 систему нормальных уравнений для выявления связи между факторным признаком – стоимость собственных оборотных средств предприятия – и результативным признаком – размер балансовой прибыли предприятия – можно записать в следующем виде:
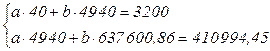
Решив систему уравнений, получаем те же значения параметров:
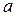 =9,097 млн. руб.;
=9,097 млн. руб.; 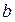 =0,574 млн. руб./млн. руб.
=0,574 млн. руб./млн. руб.
Таким образом, линейное уравнение связи принимает вид: 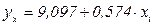 . Подставляя в него поочередно все значения стоимости СОС xi, получаем теоретические значения размера балансовой прибыли (столбец 7 таблицы 6.3). Правильность произведенных расчетов подтверждает тот факт, что сумма теоретических уровней ряда равна сумме фактических уровней:
. Подставляя в него поочередно все значения стоимости СОС xi, получаем теоретические значения размера балансовой прибыли (столбец 7 таблицы 6.3). Правильность произведенных расчетов подтверждает тот факт, что сумма теоретических уровней ряда равна сумме фактических уровней:
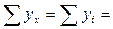 3200 млн. руб.
3200 млн. руб.
Параметр 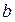 –коэффициент регрессии – показывает, что при увеличении стоимости собственных оборотных средств на 1 млн. руб. средний размер балансовой прибыли увеличивается на 0,574 млн. руб. (574 млн. руб.) и, наоборот, при снижении стоимости собственных оборотных средств на 1 млн. руб. средний размер балансовой прибыли уменьшается на 574 млн. руб.
–коэффициент регрессии – показывает, что при увеличении стоимости собственных оборотных средств на 1 млн. руб. средний размер балансовой прибыли увеличивается на 0,574 млн. руб. (574 млн. руб.) и, наоборот, при снижении стоимости собственных оборотных средств на 1 млн. руб. средний размер балансовой прибыли уменьшается на 574 млн. руб.
Коэффициент эластичности 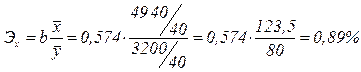 показывает, что при увеличении стоимости оборотных средств на 1% размер балансовой прибыли увеличивается на 0,89%, и наоборот.
показывает, что при увеличении стоимости оборотных средств на 1% размер балансовой прибыли увеличивается на 0,89%, и наоборот.
Оценим среднюю квадратическую ошибку уравнения регрессии ( ):
):
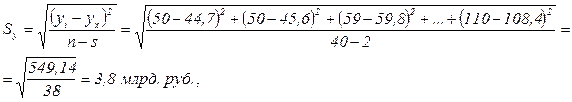
где 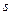 – число параметров уравнения регрессии (для уравнения прямой
– число параметров уравнения регрессии (для уравнения прямой 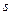 = 2).
= 2).
Поскольку  < sу (пункт 1г задания 4: sу =
< sу (пункт 1г задания 4: sу = 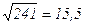 млн. руб.), то использование линейного уравнения регрессии является целесообразным.
млн. руб.), то использование линейного уравнения регрессии является целесообразным.
Нанесем фактические и теоретические значения активов, а также линию среднего размера балансовой прибыли на график (рис. 6.2).
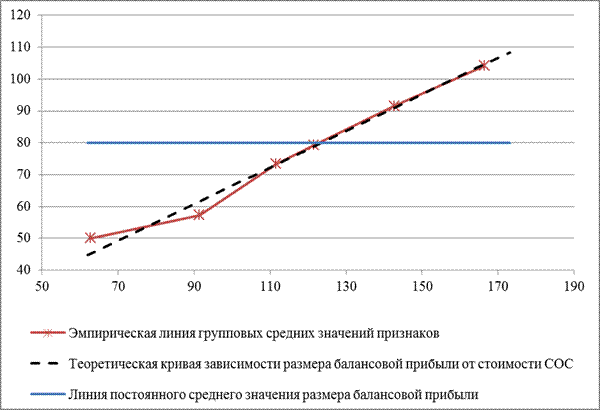
Рис. 6.2. Корреляционное поле, эмпирическая и теоретическая линии регрессии
балансовой прибыли от стоимости СОС, постоянная средняя линия
Как видно из рисунка 6.2, переменная средняя (линия теоретических значений) сильно отличается от постоянной средней, что говорит о значительном влиянии фактора х (стоимости СОС) на результативный признак y (размер балансовой прибыли). Однако несовпадение линии теоретических и фактических значений размера балансовой прибыли говорит о том, что связь между стоимостью СОС и размером балансовой прибыли не функциональная (не полная).
Измерим степень близости связи к функциональной.
3 этап. Измерение тесноты связи между признаками
Рассчитаем все виды дисперсий:
- общая дисперсия, измеряющая общую вариацию результативного признака за счет действия всех факторов:
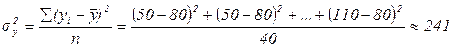 млн. руб.2
млн. руб.2
(общая дисперсия также была рассчитана в задании 4);
- факторная (теоретическая) дисперсия, измеряющая вариацию результативного признака у за счет действия только факторного признака х:
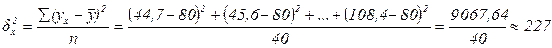 млн. руб.2
млн. руб.2
- остаточная дисперсия, характеризующая вариацию признака у за счет всех факторов, кроме х:
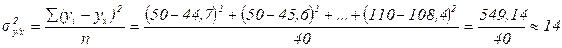 млн. руб.2
млн. руб.2
Проверим, выполняется ли правило сложения дисперсий:
 227 + 14 = 241 млн. руб.2 (верно).
227 + 14 = 241 млн. руб.2 (верно).
Оценим тесноту связи численно с помощью ряда показателей:
1. Коэффициент детерминации:
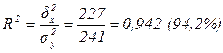 - удельный вес вариации результативного признака, линейно связанной с вариацией факторного признака, составляет 94,2%.
- удельный вес вариации результативного признака, линейно связанной с вариацией факторного признака, составляет 94,2%.
2. Индекс корреляции (теоретическое корреляционное отношение) составляет:
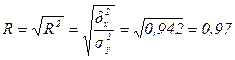 - поскольку численное значение индекса корреляции близко к единице, то линейная связь между стоимостью собственных оборотных средств и балансовой прибыли сильная (тесная).
- поскольку численное значение индекса корреляции близко к единице, то линейная связь между стоимостью собственных оборотных средств и балансовой прибыли сильная (тесная).
3. Линейный коэффициент корреляции:
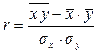 ,
,
где 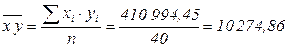 ;
;
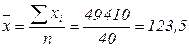 (млн. руб.);
(млн. руб.); 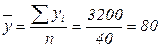 млн. руб.;
млн. руб.;
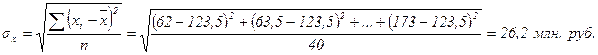
sу = 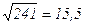 млн. руб.;
млн. руб.;
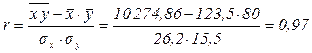 .
.
Поскольку линейный коэффициент корреляции положителен, то связь между признаками прямая, т.к. он близок к единице – связь тесная.
4 этап. Проверка существенности связи с использованием критерия Фишера:
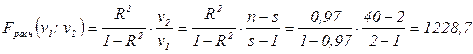
где 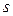 – число параметров уравнения регрессии (у прямой два параметра).
– число параметров уравнения регрессии (у прямой два параметра).
Критическое значение критерия Фишера для v1=1 и v2=38 составляет: Fкр =4,1 (прил. 2). Поскольку полученное значение Fрасч > Fкр, то существенность линейной связи между стоимостью собственных оборотных средств и размером балансовой прибыли предприятия подтверждается.
 2015-01-21
2015-01-21 557
557








