Для начала представим себе материальную точку 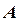 на наклонной плоскости
на наклонной плоскости 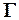 , которая по кратчайшему пути
, которая по кратчайшему пути 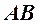 скатывается на горизонтальную плоскость проекций
скатывается на горизонтальную плоскость проекций 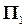 (рис.67). Понятно, что линия ската
(рис.67). Понятно, что линия ската 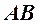 перпендикулярна линии
перпендикулярна линии 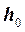 , по которой пересекаются обе плоскости
, по которой пересекаются обе плоскости 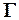 и
и 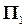 .
.
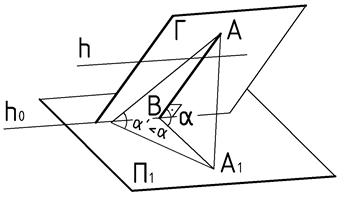
|
| Рис.67 |
Свойства линии ската:
1) Линия ската на наклонной плоскости есть линия, наибольшего наклона по отношению к горизонтальной плоскости проекций. (Из неравенства: 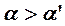 ).
).
2) Линия ската (линия наибольшего наклона) определяет угол наклона плоскости к горизонтальной плоскости проекций. (Из определения двугранного угла с учетом теоремы о проецировании прямого угла).
3) Линия ската перпендикулярна к горизонталям 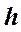 на наклонной плоскости по отношению к плоскости проекций. (Из условия параллельности любой горизонтали по отношению к линии пересечения наклонной плоскости с плоскости горизонтальной проекций:
на наклонной плоскости по отношению к плоскости проекций. (Из условия параллельности любой горизонтали по отношению к линии пересечения наклонной плоскости с плоскости горизонтальной проекций: 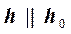 ).
).
По аналогии можно говорить о линиях наибольшего наклона относительно и других плоскостей проекций.
|
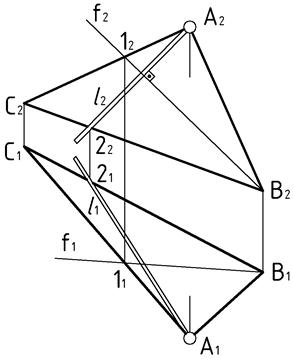
| Рис.68 |
Пример (Рис.68). Через точку 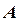 на плоскости
на плоскости 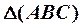 провести линию наибольшего наклона
провести линию наибольшего наклона 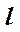 по отношению к фронтальной плоскости проекций
по отношению к фронтальной плоскости проекций 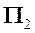 .
.
Понятно, что линия наибольшего наклона к фронтальной плоскости проекций перпендикулярна к фронталям заданной плоскости.
Дано:
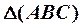 , ,
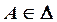 . .
| Решение:
1). 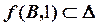 2).
2). 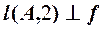 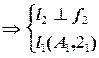 
|
?: 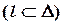 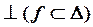 . .
|
 2014-09-04
2014-09-04 575
575








