Прямая перпендикулярна к плоскости, если она перпендикулярна (в частности) к двум линиям уровня на этой плоскости.
Прямая перпендикулярна к плоскости, если горизонтальная проекция прямой перпендикулярна к горизонтальной проекции горизонтали этой плоскости, а фронтальная проекция прямой- перпендикулярна к фронтальной проекцией фронтали. (Используются любые пары изображения перпендикуляра и с профильной проекцией. Тогда профильная проекция прямой перпендикулярна к профильной прямой плоскости).
Пример 2 (Рис.65). Через точку 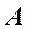 провести перпендикулярную к плоскости
провести перпендикулярную к плоскости 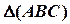 .
.
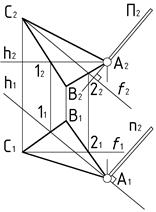 |
| Рис.65 |
Дано: 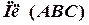 . . | Решение: 1). 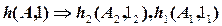 , 2). , 2). 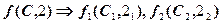 , 3). , 3). 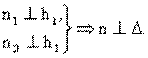 |
?: (n  A) A) 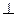 ∆. ∆. |
Пример 3 (Рис.66). Через точку 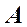 провести плоскость, перпендикулярную к плоскости
провести плоскость, перпендикулярную к плоскости 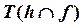 .
.
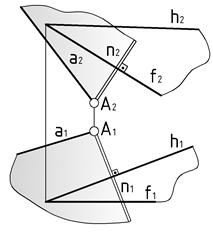 |
| Рис.66 |
Зададим искомую плоскость двумя пересекающимися прямыми. Одна из них может быть произвольная, вторая – обязательно перпендикулярной к заданной плоскости.
Дано: 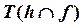 | Решение: 1). 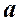 – произвольная прямая, 2). – произвольная прямая, 2). 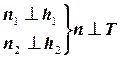 , 3). , 3). 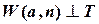 . . |
?: 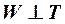 . . |
 2014-09-04
2014-09-04 749
749








