Эмпирические формулы и метод наименьших квадратов

Приближённое представление функций с помощью интерполяционных многочленов и сплайнов имеет смысл при условии, что значение приближаемой функции известны достаточно точно (т.е. при малых 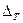). В противном случае, неустранимая погрешность настолько велика, что бессмысленно добиваться высокой теоретической точности метода. Использование интерполяционных многочленов и сплайнов при значительном числе узлов приводит к громоздким выражениям.

В тех случаях, когда значения функции определены с невысокой точностью и необходимо составить приближенное аналитическое выражение, прибегают к эмпирическим формулам: несложным формулам определенного типа. Задача состоит в выборе вида формулы, хорошо отражающей имеющиеся данные и определении её параметров.

Функция задана таблично:

			…
			…

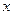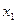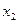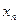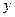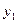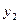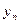Требуется найти функциональную зависимость в виде: 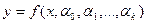(1)

где 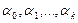неизвестные параметры.

Используются, например, формулы вида: 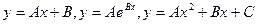и т.п.,

Параметры формул естественно стремятся определить так, чтобы отклонения 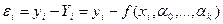были по возможности меньшими.

Требовать обращение в нуль всех 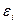нельзя, так как это приведёт к системе, содержащей гораздо больше уравнений, чем неизвестных(n уравнений при к неизвестных, где k<n). В соответствии с общей схемой вводится некоторая числовая мера близости значений 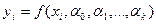к табличным значениям.

Например, можно ввести меры:

;

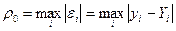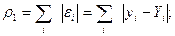
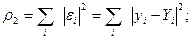
Каждая из введённых мер является функцией параметров

:

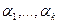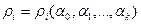
Малость каждой из них эквивалентна малости величины .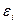

Параметры 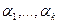определяются из условий минимума соответствующей мера. Наиболее употребительной является мера

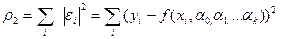(2)

Метод, определяющий параметры эмпирической формулы из условия минимума величины 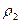, называется методом наименьших квадратов.

Из необходимых условий минимума функции нескольких переменных 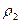следует, что в точке минимума градиент функции равен нулю.

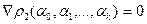(3)

т.е.в точке минимума равны нулю все её частные производные первого порядка:

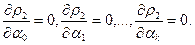(4)

Для следующих эмпирических формул:

a)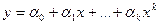

b)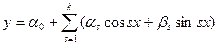

c)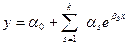

Система уравнений (4) имеет единственное решение 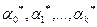и при этом функция 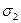принимает наименьшее значение: для любых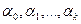

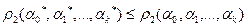
В других случаях нужно дополнительное исследование решений системы (4).

В качестве примера рассмотрим случай приближения с помощью линейной функции .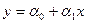

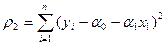. Необходимые условия минимума приводят к системе двух уравнений:

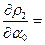
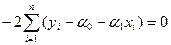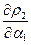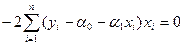, = (5)

После преобразований, получим:

,

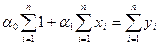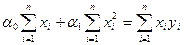
Так как 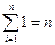, то приходим к системе

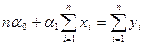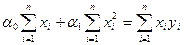, (6)

Определитель этой системы

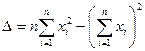можно представить в виде .

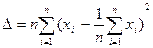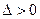всегда за исключением лишь случая, когда все принимают одно и тоже значение. Система(6) всегда имеет единственное решение, которое находится по формулам Крамера:

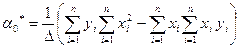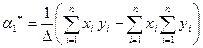; (7)

Функция 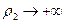при 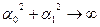, поэтому принимает наименьшее значение в точке с конечными координатами, причём точка обязательно является точкой минимума функции 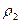. Функция 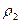имеет единственный экстремум 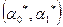, в которой функция 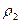принимает наименьшее значение.

Замечание. Соотношение (5) показывает, что для решения системы должно быть выполнено соотношение:

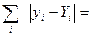
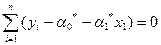
которое можно использовать для контроля вычислений.

Заметим, что для определения коэффициентов аппроксимирующей функции в виде многочлена получается система:

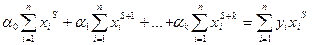
Пример 14.

Требуется определить зависимость скорости течения V от относительной глубины D по результатам десяти наблюдений приведённых в таблице.

									-
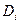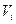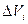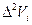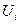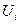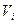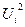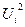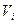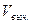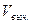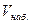(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
	0,957	0,012	-0,005	-9	-8,613		77,517	0,957
0,1	0,969		-5	-7	-6,783		47,481	0,969
0,2	0,976		-5	-5	-4,880		24,400	0,976
0,3	0,978	-3	-4	-3	-2,934		8,802	0,979	0,001
0,4	0,975	-7	-7	-1	-0,975		0,975	0,976	0,001
0,5	0,968	-14	-1		0,968		0,968	0,969	0,001
0,6	0,954	-15	-6		2,862		8,586	0,957	0,003
0,7	0,939	-21	-3		4,695		23,475	0,940	0,001
0,8	0,918	-24			6,426		44,982	0,919	0,001
0,9	0,894				8,046		72,414	0,892	-0,002
	9,528				-1,188		309,600

Для определения степени аппроксимирующего многочлена рассмотрим в столбцах (3),(4) разности. Вторые разности (4) практически постоянные, поэтому необходимо выбрать аппроксимирующий многочлен второй степени.

V=a₀+a₁D+a₂D²,

коэффициенты a_{0 ,} a₁, a_2, найдем из системы метода наименьших квадратов

10 a₀ +4,5 a₁ +2,85 a₂ =9,528,

4,5 a₀ +2,85 a₁ +2,025 a₂ =4,228,

2,85 a₀ +2,025 a₁ + 1,533 a₂ =2,65,

Решив систему уравнений получим: a₀ =0,958, a₁= 0,134, a₂ =0,228.

Искомая зависимость имеет вид:

V= 0,958 + 0,134 D+ 0,228 D²

Индивидуальные задания по методам ньютона, лагранжа, наименьших квадратов

Задание 1

1) Составить пятизначную таблицу значений функции и ее разностей до третьего порядка включительно на отрезке [ a,a+1 ] с шагом h= 0,05.

2) Проверить возможность линейной интерполяции, использую грубое условие: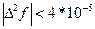

3) Написать и решить, используя компьютерную программу, систему уравнений для определения:

3.1) коэффициентов интерполяционного многочлена L₃ (x) по узлам a, a+0,25, a+05, a+0,75;

3.2) коэффициентов интерполяционного многочлена L₂ (x) по узлам a, a+0,5, a+1;

3.3) коэффициентов интерполяционного многочлена L₁ (x) по узлам a, a+1

4) Вычислить значения многочленов, полученных в п.3, в точках a+0,15 и a+0,9.

5) Сравнить их между собой и с соответствующими табличными значениями функции.

6) Составить и решить, используя компьютерную программу, систему уравнений для определения интерполяционного сплайна S₂(x) для функции f(x). За узлы сплайна принять 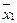=a+0,2, 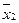=a+0,7. За узлы интерполяции принять x₀=a, x₁=a+0,5, x₂=a+1.

7) Составить формулы для вычисления значений сплайна в отрезках между узлами сплайна. Вычислить и сравнить между собой значения сплайна в точках a+0,15 и, a+0,9.

8) Сравнить величины, полученные в п.7 с соответствующими табличными значениями и со значениями интерполяционных многочленов, вычисленными в п.4.

Номер варианта	Функция	a
1 (k=1)		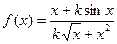1+k/2
2 (k=2)
3 (k=3)
4 (k=12)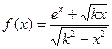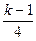
5 (k=15)
6 (k=18)
7 (k=21)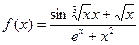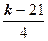
8 (k=24)
9 (k=27)
10 (k=32)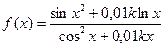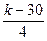
11(k=36)
12(k=40)
13(k=42)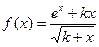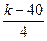
14(k=45)
15(k=50)
16(k=52)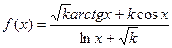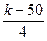
17(k=55)
18(k=60)
19(k=64)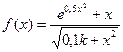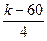
20(k=66)
21(k=70)
22(k=72)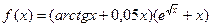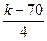
23(k=75)
24(k=80)
25(k=84)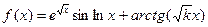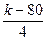
26(k=86)
27(k=88)
28(k=92)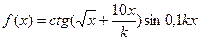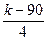
29(k=95)
30(k=100)

Задание 2

1) Для указанной функции составить таблицу значений в узлах интерполяции.

2) По заданным узлам составить интерполяционные многочлены Лагранжа и Ньютона.

3) Вычислить значения многочленов в заданной точке .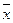

Номер варианта	Функция f(x)	Узлы интерполяции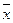
x0	x1	x2
1 (k=1)	sinx	35040’+k(205’)	x0+15’	x0+30’	x0+10’
2 (k=2)
3 (k=3)
4 (k=12)	cosx	20010’+k(1010’)	x0+20’	x0+40’	x0+10’
5 (k=15)
6 (k=18)
7 (k=21)	lnx	5,7+0,5k	x0+0,6	x0+1,2	x0+0,24
8 (k=24)
9 (k=27)
10 (k=32)		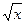123+k	x0+4	x0+8	x0+3
11(k=36)
12(k=40)
13(k=42)	ex	1+0,02k	x0+0,04	x0+0,08	x0+0,03
14(k=45)
15(k=50)
16(k=52)	tgx	400+3’k	x0+15’	x0+50’	x0+9’
17(k=55)
18(k=60)
19(k=64)	ctgx	150+2’k	x0+10’	x0+20’	x0+13’
20(k=66)
21(k=70)
22(k=72)	e-x	0,01k	x0+0,1	x0+0,2	x0+0,14
23(k=75)
24(k=80)
25(k=84)	(x3+x2+3)/(x+1)	10+0,1k	x0+1	x0+2	x0+1,3
26(k=86)
27(k=88)
28(k=92)	arcsinx	0,001k	x0+0,08	x0+0,16	x0+0,14
29(k=95)
30(k=100)

Задание 3

Для заданной таблично функции подобрать эмпирическую формулу одного из следующих видов:

1 ) y=A ;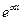

2) y=A ;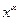

3) ;

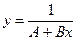4) y=A+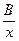

Составить и решить систему уравнений метода наименьших квадратов для определения параметров выбранной эмпирической формулы.

Значения f(x) по вариантам

НОМЕР ВАРИАНТА
x
1,0	3,3	1,4	0,56	3,5	2,7	4,0	0,3	5,0	1,3	4,0
1,5	5,7	3,3	0,43	2,6	3,1	3,0	0,24	4,7	2,2	4,6
2,0	9,8	5,8	0,36	2,5	3,6	2,5	0,2	4,5	3,7	5,4
2,3	20,0	8,0	0,32	2,4	4,0	2,3	0,2	4,4	5,0	6,1
2,5	22,0	9,5	0,30	2,3	4,2	2,2	0,18	4,4	6,1	6,3
НОМЕР ВАРИАНТА
x
1,0	0,4	2,0	1,6	1,0	0,5	9,0	2,2	3,0	0,25	1,0
1,5	0,3	1,0	2,1	1,1	0,36	7,6	6,0	3,3	0,29	2,4
2,0	0,2	1,5	2,7	1,3	0,2	7,0	11,0	3,9	0,33	3,0
2,3	0,2	1,3	3,2	1,3	0,2	6,8	29,0	4,0	0,37	3,2
2,5	0,18	1,2	3,5	1,4	0,18	6,6	45,0	4,2	0,4	3,4
НОМЕР ВАРИАНТА
x
1,0	8,0	2,1	0,11	7,0	1,4	0,7	1,0	-2,0	1,1	0,3
1,5	7,0	2,6	0,09	6,0	1,6	0,78	0,25	-0,6	1,3	1,0
2,0	6,5	3,0	0,07	5,5	1,9	0,91	0,14	0,0	1,5	2,4
2,3	6,3	3,2	0,06	5,3	2,1	0,91	0,11	0,2	1,7	3,7
2,5	6,2	3,4	0,06	5,2	2,3	0,98	0,1	0,4	1,8	4,7