Функция 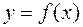 задана в равноотстоящих точках
задана в равноотстоящих точках 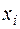 (
(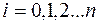 ) отрезка
) отрезка 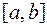 . Для нахождения производных на отрезке
. Для нахождения производных на отрезке 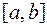 функцию
функцию 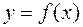 приближенно заменим интерполяционным полиномом Ньютона, построенным для системы узлов
приближенно заменим интерполяционным полиномом Ньютона, построенным для системы узлов 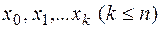 и получим первую интерполяционную формулу:
и получим первую интерполяционную формулу:
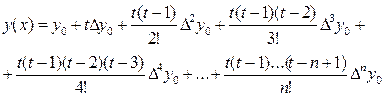 , (1)
, (1)
где 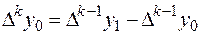 - конечная разность k-го порядка,
- конечная разность k-го порядка,
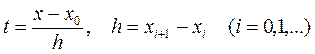 . (2)
. (2)
Перемножив биномы получим
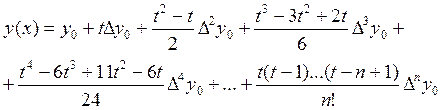 (3)
(3)
Выражение (3) содержит в правой части функцию 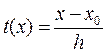 , поэтому производная имеет вид
, поэтому производная имеет вид
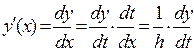
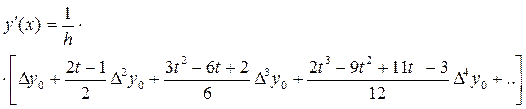

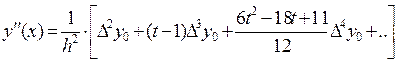
Аналогично можно вычислить производные функции 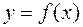 любого порядка.
любого порядка.
Представляет интерес случай, когда нужно найти производные функции 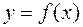 в основных табличных точках
в основных табличных точках 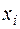 . Каждое табличное значение можно принять за начальное
. Каждое табличное значение можно принять за начальное 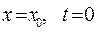 , тогда производная в точке
, тогда производная в точке 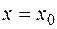 будет иметь вид
будет иметь вид
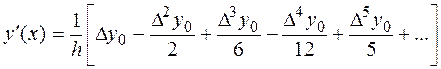
и
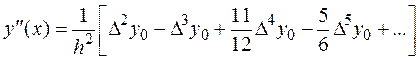 .
.
Если 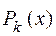 - интерполяционный полином Ньютона, содержащий разности
- интерполяционный полином Ньютона, содержащий разности 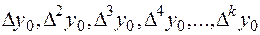 , и соответствующая погрешность вычисляется по формуле
, и соответствующая погрешность вычисляется по формуле 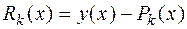 , то погрешность в определении производной есть
, то погрешность в определении производной есть 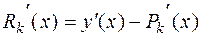 .
.
Пример. Найти значение производной функции 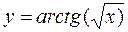
в точке 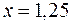 с помощью численных методов.
с помощью численных методов.
Сформируем диагональную таблицу конечных разностей заданной функции
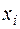 | 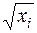 | 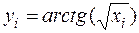 | 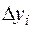 | 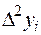 | 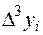 | 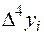 |
| 0,2000 | 0,4472 | 0,4205 | ||||
| 0,4000 | 0,6325 | 0,5639 | 0,1434 | |||
| 0,6000 | 0,7746 | 0,6591 | 0,0951 | -0,0483 | ||
| 0,8000 | 0,8944 | 0,7297 | 0,0707 | -0,0244 | 0,0238 | |
| 1,0000 | 1,0000 | 0,7854 | 0,0557 | -0,0150 | 0,0094 | -0,0144 |
| 1,2000 | 1,0954 | 0,8309 | 0,0455 | -0,0102 | 0,0048 | -0,0046 |
| 1,4000 | 1,1832 | 0,8691 | 0,0382 | -0,0073 | 0,0028 | -0,0020 |
| 1,6000 | 1,2649 | 0,9018 | 0,0327 | -0,0055 | 0,0018 | -0,0010 |
| 1,8000 | 1,3416 | 0,9303 | 0,0284 | -0,0043 | 0,0012 | -0,0006 |
| 2,0000 | 1,4142 | 0,9553 | 0,0250 | -0,0034 | 0,0009 | -0,0004 |
| 2,2000 | 1,4832 | 0,9776 | 0,0223 | -0,0028 | 0,0006 | -0,0002 |
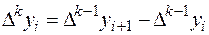 .
.
Возьмем ближайшее к заданному значению 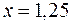 табличное значение
табличное значение 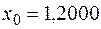 , тогда
, тогда 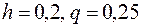 ,
,
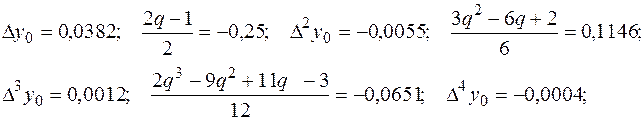
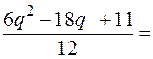 0,5729.
0,5729.
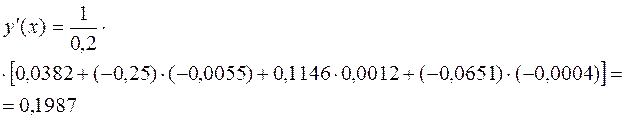
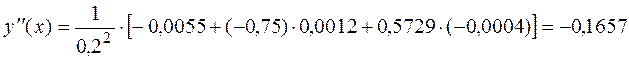
Найдем производную заданной функции аналитически и сравним полученные результаты.
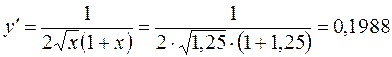
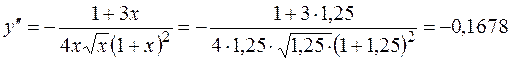
 2015-01-21
2015-01-21 4598
4598








