Формулы численного дифференцирования, рассмотренные ранее используют лишь значения функции при 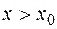 . Более точный результат дают центральные формулы дифференцирования, которые учитывают значения данной функции как при
. Более точный результат дают центральные формулы дифференцирования, которые учитывают значения данной функции как при 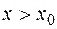 , так и при
, так и при 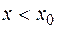 . Одна из подобных формул получается, если взять за основу интерполяционную формулу Стирлинга.
. Одна из подобных формул получается, если взять за основу интерполяционную формулу Стирлинга.
Пусть 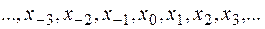 - система равноотстоящих точек с шагом
- система равноотстоящих точек с шагом 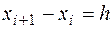 . Значения данной функции в этих точках
. Значения данной функции в этих точках 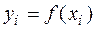 . Заменив приближенно заданную функцию интерполяционным полиномом Стирлинга, получим:
. Заменив приближенно заданную функцию интерполяционным полиномом Стирлинга, получим:

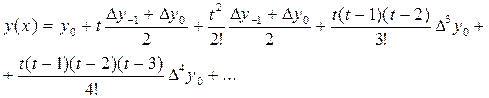
Формула численного дифференцирования, основанная на формуле Стирлинга имеет вид
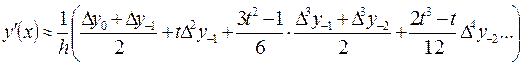
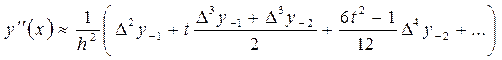
Пример. Вычислить значение первой и второй производных при 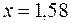 . В таблице берем
. В таблице берем 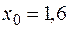 .
.
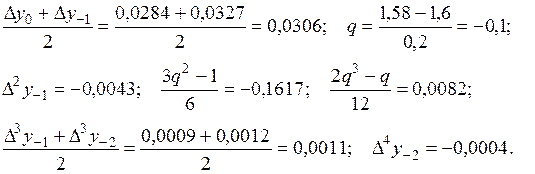
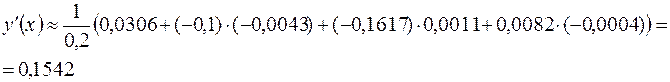

 2015-01-21
2015-01-21 2206
2206








