2015-01-21
525
Если функция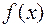 
непрерывна на отрезке 
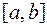и известна ее первообразная 
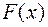, то определенный интеграл от этой функции на заданном отрезке вычисляется по формуле Ньютона – Лейбница 
.
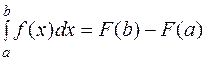Во многих случай первообразная функции не может быть найдена аналитически, либо является слишком сложной. На практике подынтегральная функция часто задается таблично и тогда само понятие первообразной не имеет смысла. Большое значение имеют приближенные и в первую очередь численные методы вычисления определенных интегралов. Задача численного интегрирования функции заключается в вычислении значения определенного интеграла на основании ряда значений подынтегральной функции. Численное вычисление однократного интеграла называется механической квадратурой, двойного – механической кубатурой. Соответствующие формулы называются квадратурными и кубатурными формулами. Метод состоит в том, что данную функцию 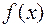на рассматриваемом отрезке 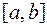заменяют интерполирующей или аппроксимирующей функцией 
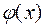простого вида (например, полиномом) и полагают
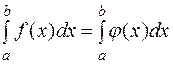
Функция 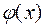должна быть такова, чтобы интеграл 
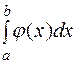вычислялся непосредственно.
