Дифференциальные уравнения второго порядка, приводимые
1. Дифференциальные уравнения вида 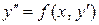 , в которых функция
, в которых функция 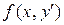 не зависит от y, решаются с помощью подстановки
не зависит от y, решаются с помощью подстановки 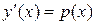 .
.
Находим 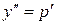 и подставляем в исходное уравнение, получаем дифференциальное уравнение относительно p
и подставляем в исходное уравнение, получаем дифференциальное уравнение относительно p  . Если удастся найти решение данного уравнения
. Если удастся найти решение данного уравнения  , то решение исходного уравнения найдется как интеграл
, то решение исходного уравнения найдется как интеграл 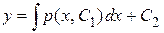 .
.
Пример 7.17. Решить уравнение 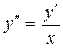 при
при 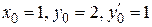 .
.
Принимаем 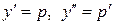 . Уравнение примет вид
. Уравнение примет вид 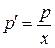 .
.
Разделим переменные 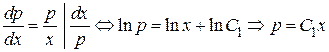 .
.
Далее интегрируем уравнение  .
.
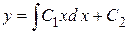 .
.
Получаем общее решение 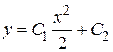 .
.
Находим частное решение. Из уравнения  находим
находим 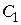 .
.
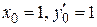 ;
; 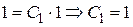 .
.
Из общего решения 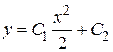 находим
находим 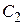 .
.
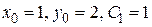 ;
; 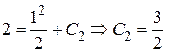 .
.
Частное решение 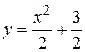 .
.
2. Дифференциальные уравнения вида 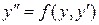 , не содержащие в явном виде x, решаются с помощью замены
, не содержащие в явном виде x, решаются с помощью замены 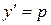 . Производную
. Производную 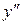 в данном случае представим в виде
в данном случае представим в виде
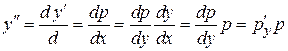 .
.
В результате замены уравнение приобретает вид 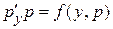 . Если удается найти общее решение этого уравнения
. Если удается найти общее решение этого уравнения 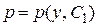 , то далее интегрируют уравнение
, то далее интегрируют уравнение 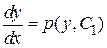 . Данное уравнение с разделяющимися переменными. Разделим переменные и проинтегрируем
. Данное уравнение с разделяющимися переменными. Разделим переменные и проинтегрируем 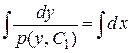 , найдем общий интеграл
, найдем общий интеграл
 .
.
Пример 7.18. Решить уравнение 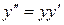 .
.
Выполняем замену 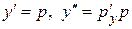 , получаем
, получаем 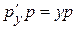 или
или 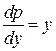 . Разделяем переменные
. Разделяем переменные 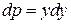 и интегрируем
и интегрируем 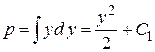 .
.
Так как 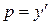 , далее необходимо решить уравнение
, далее необходимо решить уравнение 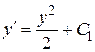 .
.
Находим 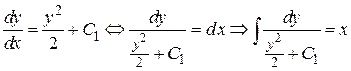 .
.
В зависимости от начальных условий 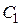 может принять либо положительное, либо отрицательное значение.
может принять либо положительное, либо отрицательное значение.
Если 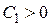 , то
, то  , и общий интеграл уравнения имеет вид
, и общий интеграл уравнения имеет вид  .
.
Если 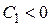 , то
, то 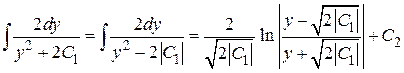 и
и
общий интеграл имеет вид 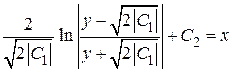 .
.
7.12. Линейные дифференциальные уравнения n -ого порядка. Свойства их решений
В общем случае данные уравнения имеют вид
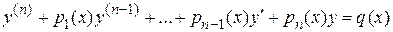 ,
,
где 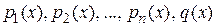 - непрерывные функции.
- непрерывные функции.
Обозначим левую часть дифференциального уравнения, линейную относительно y и ее производных через 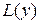 , т. е.
, т. е.
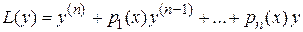 .
.
Тогда уравнение можно записать в виде 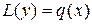 . Этому неоднородному уравнению соответствует однородное уравнение
. Этому неоднородному уравнению соответствует однородное уравнение 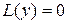 .
.
Свойство 1. Если 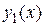 и
и 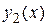 являются решениями однородного уравнения
являются решениями однородного уравнения 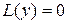 , то их сумма
, то их сумма 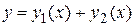 также является решением этого уравнения. Действительно, в силу линейности функции
также является решением этого уравнения. Действительно, в силу линейности функции 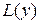
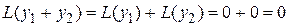 .
.
Свойство 2. Если 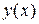 является решением уравнения
является решением уравнения 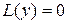 , то
, то 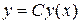 , где
, где 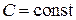 , также является решением этого уравнения.
, также является решением этого уравнения.
Действительно, 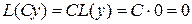 .
.
Свойство 3. Если 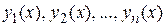 являются решениями уравнения
являются решениями уравнения 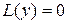 , то
, то 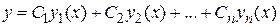 , где
, где 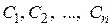 - постоянные также является решением этого уравнения.
- постоянные также является решением этого уравнения.
В силу линейности уравнения имеем
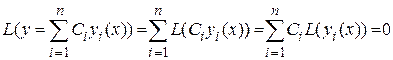 .
.
Свойство 4. Если 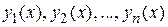 являются решениями однородного уравнения
являются решениями однородного уравнения 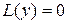 , а
, а  решением неоднородного уравнения
решением неоднородного уравнения 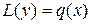 , то
, то 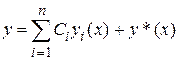 также является решением неоднородного уравнения.
также является решением неоднородного уравнения.
Действительно,
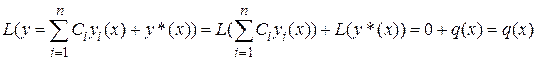 .
.
 2014-02-02
2014-02-02 551
551








