2014-02-03
3661
При решении задачи поиска оптимального управления функционал качества можно записать в виде:
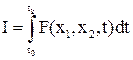или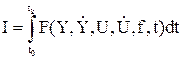 
Если дать приращение координатам состояния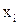 
(проварьировать их), то изменится значение функционала качества. Причем варьирование координат производится так: направление 
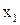меняется произвольно в классе гладких функций на интервале 
, 
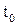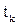, а граничные значения функции 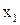должны оставаться постоянными, т.е. совпадать.
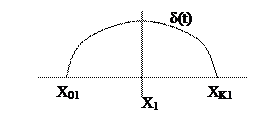
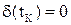и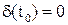 
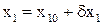
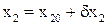
Вместо координат 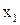и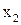 
подставляем эти значения в подынтегральную функцию функционала качества
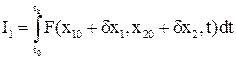
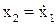
Тогда
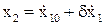
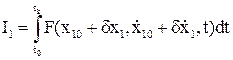
Найдем приращение функционала качества при варьировании аргументов
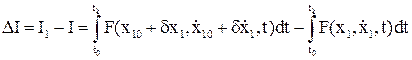
Вариационная формула представляется в виде ряда Тейлора:
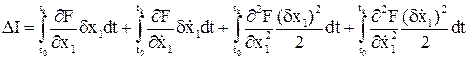
Т.к. вариации аргументов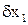 
и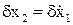 
малы, то вторые и высшие производные в этом разложении отбрасывают
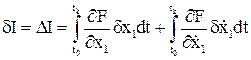
Линейную часть приращения функционала называют первой вариацией функционала и обозначают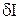 
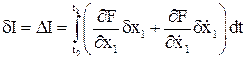
Необходимым условием существования экстремума функционала качества является равенство нулю его первой вариации
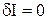
В этом выражении проинтегрируем по частям второе слагаемое:
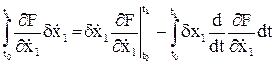
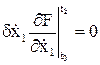
Полученное выражение подставляем в выражение для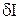
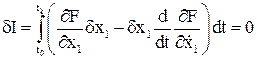
Т.е. для того, чтобы 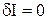, необходимо, чтобы:
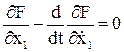
Если переменных много, то
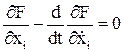– уравнение Эйлера.
Если функционал качества зависит от управления, можно дописать:
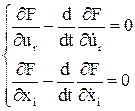– система уравнений Эйлера, решив которую находят управление.
Кривые изменения координат состояния, при которых получаются экстремумы функционала качества, называются экстремальными.
Систему уравнений Эйлера можно использовать тогда, когда координаты состояния и управления являются непрерывными гладкими функциями и не имеют ограничений типа неравенств.
Если управление выбирается из класса разрывных функций и на управление наложено ограничение в виде неравенств и на координаты состояния наложено ограничение самим уравнением ОУ, то задача сводится к поиску условного экстремума функции многих переменных. В этом случае координаты состояния и управления, связанные уравнением объекта, не могут варьироваться независимо. В этом случае составляют функцию Лагранжа и систему уравнений Эйлера, но только для функции Лагранжа, т.е. подынтегральная функция функционала другая.
Задача формулируется следующим образом:
Определить оптимальное управление, обеспечивающее экстремум функционала качества, в котором координаты состояния и управления связываются уравнением объекта в виде уравнений состояния.
Функционал:
;
.
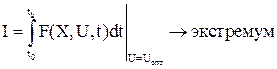
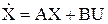
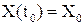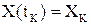Подынтегральная функция функционала качества должна быть непрерывной по всем переменным и должна иметь непрерывные частные производные до 2-го порядка включительно. При использовании системы уравнений Лагранжа подынтегральная функция функционала качества записывается следующим образом:
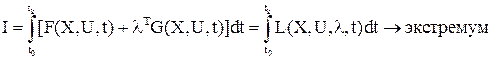
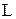– функция Лагранжа
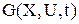– уравнение связи, которое накладывается на 
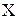и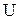 
.
Для определения оптимального управления составляется система уравнений Эйлера для функций Лагранжа. Эта система называется системой уравнений Эйлера-Лагранжа.
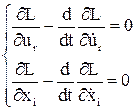
Решение задачи усложняется тем, что неизвестны начальные значения множителей Лагранжа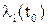 
и чтобы удовлетворять заданным значениям конечного и начального состояния 
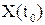и 
приходится многократно решать уравнения вариационной задачи, задаваясь различными значениями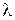 
.
Уравнения вариационной задачи могут быть записаны в канонической (гамильтоновой) форме.
Система уравнений Эйлера.
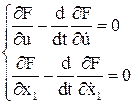
Новые канонические переменные:
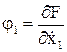
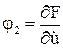
Вместо подынтегральной функции функционала качества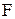 
записывают функцию Гамильтона:
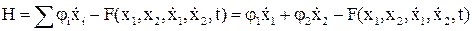
Тогда система уравнений:
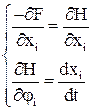
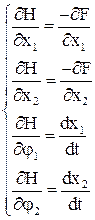
На основании уравнений Эйлера:
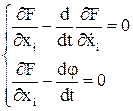
Тогда система уравнений для решения вариационной задачи:
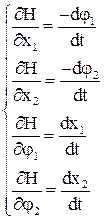
Или в общем виде:
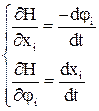
Для общей задачи Лагранжа
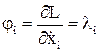
Тогда функцию Гамильтона при решении задачи с помощью уравнений Эйлера-Лагранжа запишем:
,
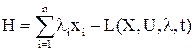а система уравнений будет выглядеть следующим образом:
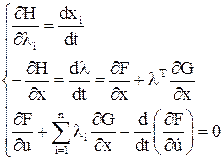
(из нее находится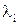 
, а потом 
)
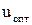Если решается задача с помощью системы уравнений Эйлера-Лагранжа, то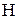 
-функцию можно не использовать.
Пример:
Определить оптимальное управление для объекта, заданного следующей передаточной функцией:
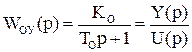в процессе перевода его из начального положения 
, 
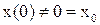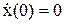в конечное состояние 
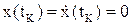, обеспечивающее минимум функционала качества:
, причем коэффициенты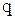 
и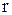 
положительны.
Решение:
1. Запишем уравнение объекта в форме Коши
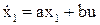
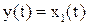
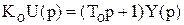
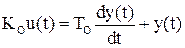
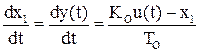
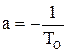
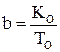
2. Составим функцию Лагранжа
Поскольку ограничение координат задается всегда уравнением объекта
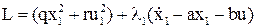
3. Составляем систему уравнений Эйлера-Лагранжа
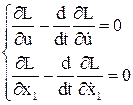
Эти два уравнения дополняются уравнением объекта
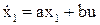
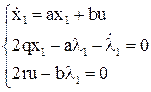
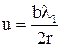
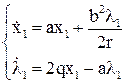
Для определения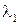 
нужно определить корни этой системы уравнений.
Для этого составляем матрицу:
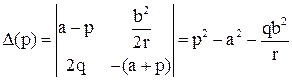
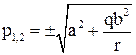
Уравнение ОУ первого порядка. Должен быть один корень. Из условий устойчивости выбираем отрицательный корень. Тогда решение системы уравнений принимает вид:
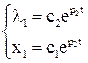
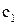– постоянная интегрирования, которая определяется по заданным начальным условиям объекта;
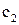– определяется значением 
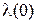, а оно неизвестно.
Для определения 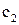подставим в найденное выражение для 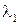и 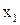в уравнение объекта:
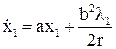
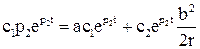
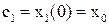
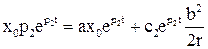
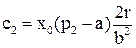
Подставим 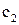в выражение для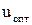
Это говорит о том, что оптимальное управление изменяется по такому же закону как и выходная координата объекта, следовательно, оптимальное управление является функцией фазовых координат:
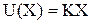
Получается, что закон регулирования формируется с помощью ОС по выходной координате.
