| Понятие | Определение и назначение | Геометрическое изображение | Вычисление |
1.Векторное поле 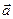 | Каждой точке 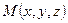 соответствует значение векторной функции соответствует значение векторной функции 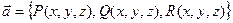 | 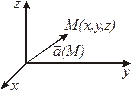 | 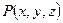 , , 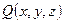 , ,  – проекция вектора – проекция вектора 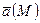 на оси на оси 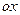 , , 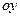 , , 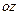 |
2.векторная (силовая) линия поля 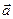 | Линия, во всякой точке которой вектор 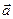 направлен по касательной к ней. направлен по касательной к ней. |  | 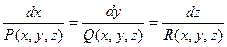 Система дифференциальных уравнений, определяющая векторные линии Система дифференциальных уравнений, определяющая векторные линии |
3.Поток поля 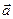 через поверхность Q через поверхность Q | 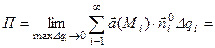 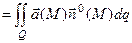 где где 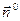 - единичный вектор нормали к поверхности - единичный вектор нормали к поверхности | 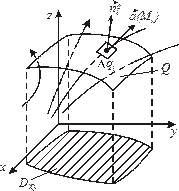 | 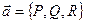 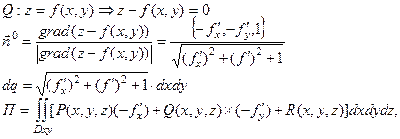 где где 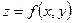 |
| 4. Дивергенция поля (расходимость поля) | 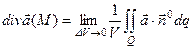 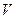 -объем, ограниченный поверхностью -объем, ограниченный поверхностью |  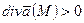 ; ; 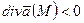 т. т. 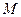 - исток; т. - исток; т. 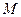 - сток - сток | 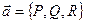 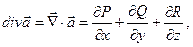 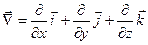 - оператор Гамильтона, ( - оператор Гамильтона, (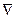 - набла) Поле - набла) Поле 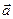 - соленоидальное (трубчатое), если - соленоидальное (трубчатое), если 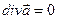 |
5. Поток поля 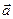 через замкнутую поверхность через замкнутую поверхность 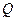 | Формула Гаусса – Остроградского (связь между потоком и дивергенцией поля) 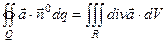 | 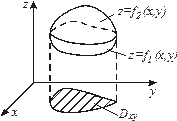 | 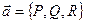 R: R: 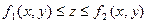 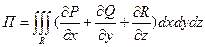 |
6. Ротор (вихрь) поля 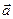 | 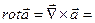 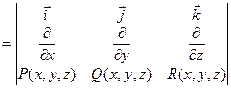 | | 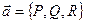 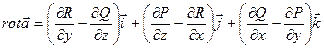 Поле Поле 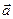 (M) – потенциальное (безвихревое) если (M) – потенциальное (безвихревое) если 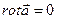 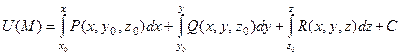 - потенциал поля - потенциал поля 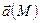 |
7. Работа поля 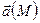 по перемещению точки вдоль кривой по перемещению точки вдоль кривой 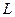 | 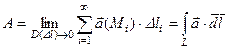 | 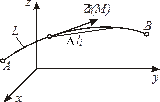 | 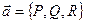 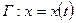 , , 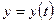 , , 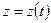 , , 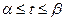 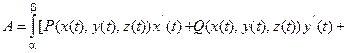 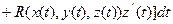 |
8. Циркуляция поля 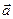 по контуру по контуру 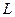 | 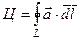 |  | Вычисляется аналогично пункту 7. А=Ц, если Г – замкнутый контур. (В потенциальном поле Ц=0). |
9. Циркуляция поля 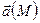 по замкнутому контуру по замкнутому контуру 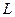 , являющемся границей поверхности , являющемся границей поверхности 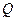 | Формула Стокса устанавливает связь потока вектора 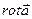 с циркуляцией поля с циркуляцией поля 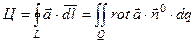 |  | 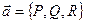 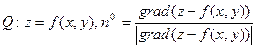 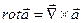 (см п. 5), (см п. 5), 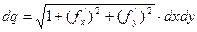 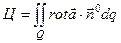 вычисляется как в пункте 3 вычисляется как в пункте 3 |
10.Циркуляция плоского поля 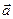 по замкнутому контуру по замкнутому контуру 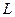 | Формула Грина устанавливает связь вихря с циркуляцией плоского поля 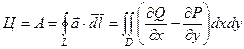 | 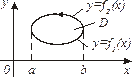 | 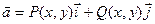 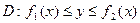 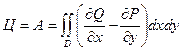 |
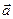
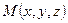 соответствует значение векторной функции
соответствует значение векторной функции 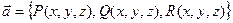
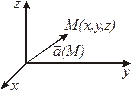
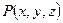 ,
, 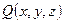 ,
,  – проекция вектора
– проекция вектора 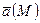 на оси
на оси 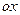 ,
, 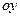 ,
, 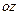
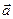
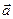 направлен по касательной к ней.
направлен по касательной к ней. 
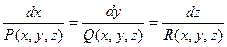 Система дифференциальных уравнений, определяющая векторные линии
Система дифференциальных уравнений, определяющая векторные линии 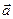 через поверхность Q
через поверхность Q 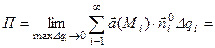
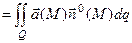 где
где 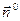 - единичный вектор нормали к поверхности
- единичный вектор нормали к поверхности 
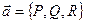
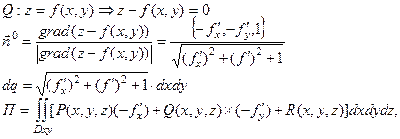 где
где 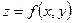
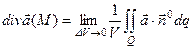
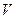 -объем, ограниченный поверхностью
-объем, ограниченный поверхностью 
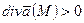 ;
; 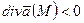 т.
т. 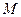 - исток; т.
- исток; т. 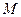 - сток
- сток 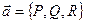
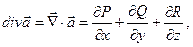
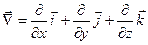 - оператор Гамильтона, (
- оператор Гамильтона, (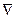 - набла) Поле
- набла) Поле 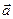 - соленоидальное (трубчатое), если
- соленоидальное (трубчатое), если 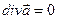
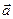 через замкнутую поверхность
через замкнутую поверхность 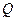
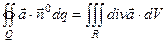

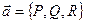 R:
R: 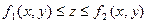
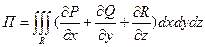
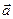
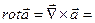
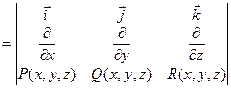
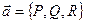
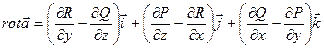 Поле
Поле 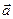 (M) – потенциальное (безвихревое) если
(M) – потенциальное (безвихревое) если 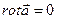
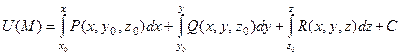 - потенциал поля
- потенциал поля 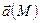
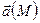 по перемещению точки вдоль кривой
по перемещению точки вдоль кривой 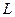
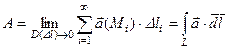

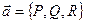
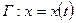 ,
, 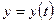 ,
, 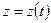 ,
, 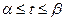
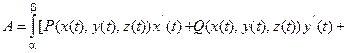
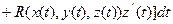
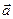 по контуру
по контуру 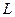
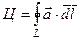

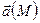 по замкнутому контуру
по замкнутому контуру 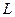 , являющемся границей поверхности
, являющемся границей поверхности 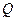
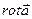 с циркуляцией поля
с циркуляцией поля 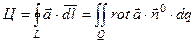

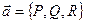
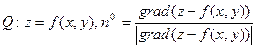
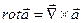 (см п. 5),
(см п. 5), 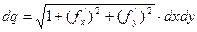
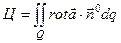 вычисляется как в пункте 3
вычисляется как в пункте 3 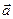 по замкнутому контуру
по замкнутому контуру 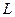
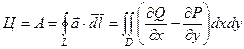

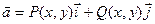
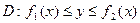
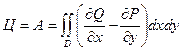
 2015-01-21
2015-01-21 1319
1319








