Вид уравнения: 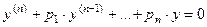 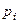 - числа - числа | Характер корней характеристического уравнения | |
Корни действительные, различные, т. е. 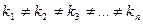 | Корни действительные, есть повторяющиеся, т.е. 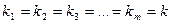 (корень кратности m) (корень кратности m) | Корни комплексные, различные 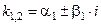 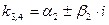 и т. д. и т. д. | Корни комплексные, есть повторяющиеся 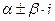 - пара корней кратности - пара корней кратности 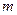 | |
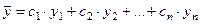 - общее решение денного уравнения, где - общее решение денного уравнения, где 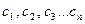 - произвольные постоянные, - произвольные постоянные, 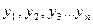 - фундаментальная система решений данного уравнения. - фундаментальная система решений данного уравнения. | Вид частных решений 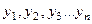 , соответствующих корням характеристического уравнения , соответствующих корням характеристического уравнения | |
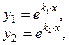 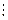 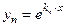 | 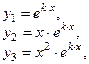 , , 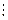 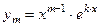 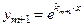 ............ ............ | 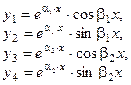 ............ ............ | 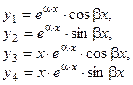 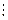 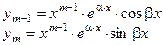 | |
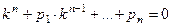 - характеристическое уравнение - характеристическое уравнение | |
22. Линейные неоднородные дифференциальные уравнения n-го порядка
с постоянными коэффициентами
Вид уравнения: 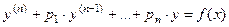 | Метод вариации произвольных постоянных | Метод подбора частного решения | |
Если 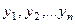 - фундаментальная система решений соответствующего однородного уравнения, то общее решение неоднородного уравнения находится по формуле - фундаментальная система решений соответствующего однородного уравнения, то общее решение неоднородного уравнения находится по формуле 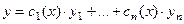 , если , если 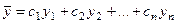 где где 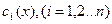 находится из системы уравнений находится из системы уравнений 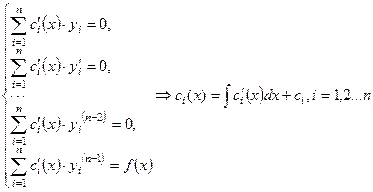 Частный случай: Частный случай: 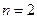 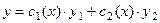 , , 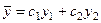 где где 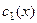 и и 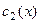 находятся из системы уравнений находятся из системы уравнений 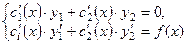 Þ найти Þ найти 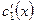 и и 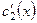 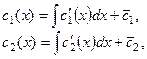 где где 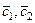 - постоянные - постоянные | 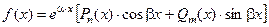 - специальный вид правой части неоднородного уравнения (пусть - специальный вид правой части неоднородного уравнения (пусть 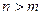 ) Частное решение ) Частное решение 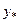 ищется в виде ищется в виде 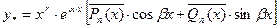 , где , где 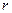 – кратность корней – кратность корней 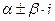 характеристического уравнения: характеристического уравнения: 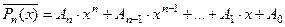 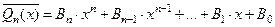 То есть То есть 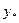 зависит от правой части зависит от правой части 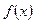 и от корней характеристического уравнения. и от корней характеристического уравнения. | |
Структура общего решения: 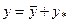 , где , где 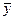 - общее решение соответствующего однородного уравнения, - общее решение соответствующего однородного уравнения, 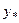 - частное решение неоднородного уравнения. - частное решение неоднородного уравнения. | |
Если 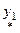 - частное решение уравнения - частное решение уравнения 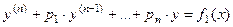 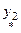 - частное решение уравнения - частное решение уравнения 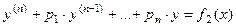 , то , то 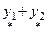 - частное решение уравнения - частное решение уравнения 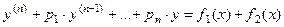 | |
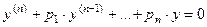
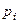 - числа
- числа 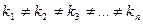
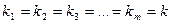 (корень кратности m)
(корень кратности m) 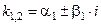
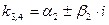 и т. д.
и т. д. 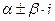 - пара корней кратности
- пара корней кратности 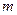
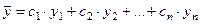 - общее решение денного уравнения, где
- общее решение денного уравнения, где 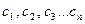 - произвольные постоянные,
- произвольные постоянные, 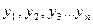 - фундаментальная система решений данного уравнения.
- фундаментальная система решений данного уравнения. 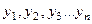 , соответствующих корням характеристического уравнения
, соответствующих корням характеристического уравнения 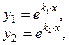
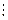
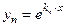
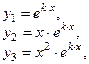 ,
, 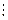
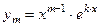
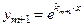 ............
............ 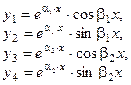 ............
............ 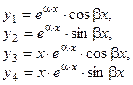
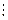
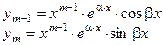
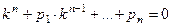 - характеристическое уравнение
- характеристическое уравнение 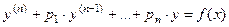
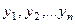 - фундаментальная система решений соответствующего однородного уравнения, то общее решение неоднородного уравнения находится по формуле
- фундаментальная система решений соответствующего однородного уравнения, то общее решение неоднородного уравнения находится по формуле 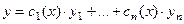 , если
, если 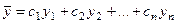 где
где 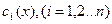 находится из системы уравнений
находится из системы уравнений 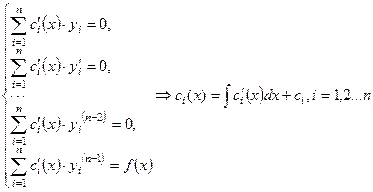 Частный случай:
Частный случай: 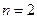
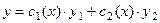 ,
, 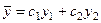 где
где 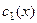 и
и 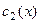 находятся из системы уравнений
находятся из системы уравнений 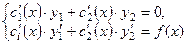 Þ найти
Þ найти 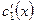 и
и 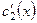
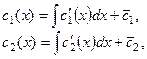 где
где 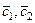 - постоянные
- постоянные 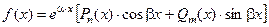 - специальный вид правой части неоднородного уравнения (пусть
- специальный вид правой части неоднородного уравнения (пусть 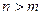 ) Частное решение
) Частное решение 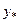 ищется в виде
ищется в виде 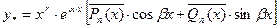 , где
, где 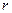 – кратность корней
– кратность корней 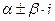 характеристического уравнения:
характеристического уравнения: 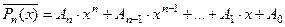
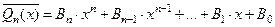 То есть
То есть 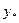 зависит от правой части
зависит от правой части 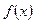 и от корней характеристического уравнения.
и от корней характеристического уравнения. 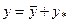 , где
, где 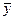 - общее решение соответствующего однородного уравнения,
- общее решение соответствующего однородного уравнения, 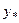 - частное решение неоднородного уравнения.
- частное решение неоднородного уравнения. 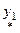 - частное решение уравнения
- частное решение уравнения 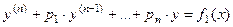
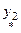 - частное решение уравнения
- частное решение уравнения 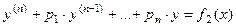 , то
, то 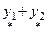 - частное решение уравнения
- частное решение уравнения 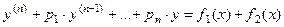
 2015-01-21
2015-01-21 1087
1087
