Определение: Коэффициентом корреляции (KK) двух случайных величин x1, x2 называется 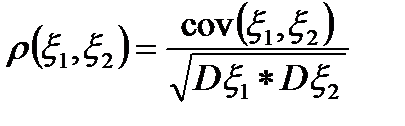 .
.
Свойства KK:
1. r - величина безразмерная.
2. |r|£1, в силу (**).
3. Модуль коэффициента корреляции равен единице тогда и только тогда, когда x 1, x 2 связаны линейной функциональной зависимостью, т.е. |r|=1 Û x2 = a*x1+b.
4. если x1, x2 независимы, то r=0 (но не наоборот, так как r - мера линейной связи между двумя случайными величинами, может быть, что связь существенно нелинейная, r=0).
5. если x1, x2 подчиняются двумерному нормальному закону распределения, то понятия некоррелированности и независимости идентичны.
6. |r| не изменится, если x1, x2 в отдельности подвергнуть линейному преобразованию: т.е. если h1= а1x1+b1 , h2 =a2x2+b2, то |r(h1,h2)|=|r(x1,x2)|.
Пусть в роли X и Y выступают произвольные столбцы стандартизованной матрицы данных (их средние равны нулю, а дисперсии - единице). 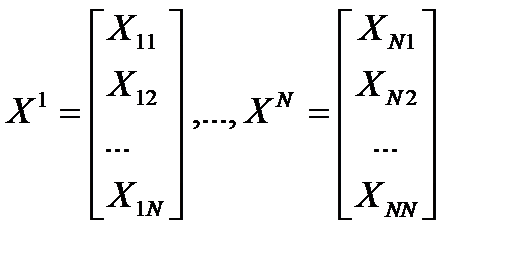 , тогда выборочный коэффициент корреляции между i- ым и j- ым столбцами.
, тогда выборочный коэффициент корреляции между i- ым и j- ым столбцами.
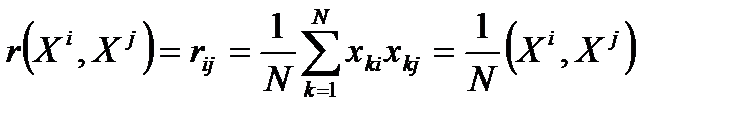
32.
Рассмотрим случайную величину Х такую, что 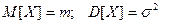 . Тогда для любого
. Тогда для любого 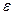 >0
>0
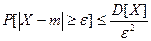 .
.
Это неравенство называется неравенством Чебышева.
Пример 3.3. Оценить вероятность того, что 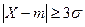 для произвольного распределения случайной величины.
для произвольного распределения случайной величины.
Решение. Пользуясь неравенством Чебышева и полагая 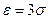 , получим:
, получим:
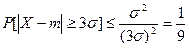 .
.
Сравнивая полученную оценку с законом трех сигм для нормального распределения, заметим, что неравенство Чебышева дает другую оценку вероятности выполнения данного соотношения. Это является следствием того, что данное неравенство верно для любого распределения случайной величины. Поэтому неравенство Чебышева не имеет практической ценности, а используется в теоретических выкладках, в частности для доказательства теоремы Чебышева.
Неравенство Чебышева можно записать в другом виде:
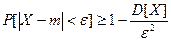 Рассмотрим последовательность случайных величин Х 1, Х 2,.., Хn. Говорят, что данная последовательность случайных величин сходится по вероятности к числу m, если для любого
Рассмотрим последовательность случайных величин Х 1, Х 2,.., Хn. Говорят, что данная последовательность случайных величин сходится по вероятности к числу m, если для любого 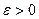
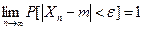 .В этом случае записывают:
.В этом случае записывают:  .
.
Теорема Чебышева (закон больших чисел). Если Х 1, Х 2,.., Хn – попарно независимые случайные величины, причем 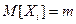 , а дисперсия
, а дисперсия 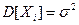 - равномерно ограниченная (то есть не превышает некоторого постоянного числа С для любого
- равномерно ограниченная (то есть не превышает некоторого постоянного числа С для любого  ), то
), то
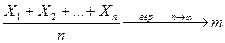 ,
,
то есть для любого 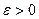
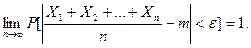
Таким образом, теорема Чебышева утверждает, что при данных условиях при достаточно большом числе случайных величин их среднее арифметическое мало отличается от математического ожидания той случайной величины, среднее арифметическое которой вычисляется.
Сущность теоремы Чебышева такова: хотя отдельные независимые случайные величины могут принимать значения, далекие от своих математических ожиданий, среднее арифметическое достаточно большого числа случайных величин с большой вероятностью принимает значение, близкое к математическому ожиданию случайных величин, входящих в сумму.
Другими словами, отдельные случайные величины могут иметь значительный разброс, в то время как их среднее значение рассеяно мало, т.е. среднее арифметическое достаточно большого числа случайных величин утрачивает характер случайно величины.
34.
В центральной предельной теореме описываются условия, при которых возникает нормальный закон распределения. Оказывается, что он возникает всякий раз, когда случайная величина может быть представлена в виде суммы достаточно большого числа попарно независимых случайных величин, каждая из которых сравнительно мало влияет на всю сумму.
Пусть случайные величины 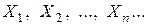 (*) попарно независимы и каждая из них обладает математическим ожиданием и дисперсией:
(*) попарно независимы и каждая из них обладает математическим ожиданием и дисперсией: 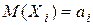 ,
, 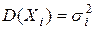 . Обозначим через Sn сумму
. Обозначим через Sn сумму 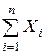 , через Аn сумму
, через Аn сумму 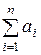 , через Bn сумму
, через Bn сумму 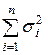 .
.
Будем говорить, что к последовательности (*) применима центральная предельная теорема, если для любых чисел t 1, t 2, 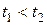 при
при 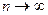 справедливо предельное соотношение
справедливо предельное соотношение
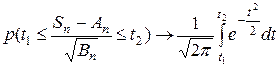 ,
, 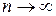 .
.
Иными словами, при 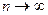 случайная величина Sn имеет приближенно нормальное распределение с параметрами а =
случайная величина Sn имеет приближенно нормальное распределение с параметрами а = 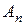 и s =
и s = 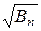 .
.
Теорема Ляпунова. В этой теореме устанавливаются достаточно общие условия, выполнение которых влечет применимость центральной предельной теоремы к последовательности (*). Эти условия охватывают большинство практических случаев.
Будем дополнительно предполагать, что у случайных величин Хi существуют абсолютные центральные моменты третьей степени  . Если для последовательности (*) справедливо предельное соотношение
. Если для последовательности (*) справедливо предельное соотношение 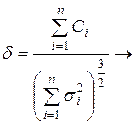 0,
0, 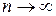 , то для последовательности (*) справедлива и центральная предельная теорема.
, то для последовательности (*) справедлива и центральная предельная теорема.
Можно показать, что если 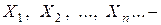 одинаково распределенные и независимые случайные величины, то для последовательности (*) справедлива центральная предельная теорема.
одинаково распределенные и независимые случайные величины, то для последовательности (*) справедлива центральная предельная теорема.
35. Пусть в каждом из 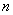 независимых испытаний событие A может произойти с вероятностью
независимых испытаний событие A может произойти с вероятностью 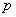 ,
, 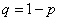 (условия схемы Бернулли). Обозначим как и раньше, через
(условия схемы Бернулли). Обозначим как и раньше, через 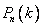 вероятность ровно
вероятность ровно 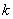 появлений события А в
появлений события А в 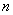 испытаниях. кроме того, пусть
испытаниях. кроме того, пусть 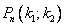 – вероятность того, что число появлений события А находится между
– вероятность того, что число появлений события А находится между 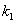 и
и 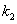 .
.
 2015-01-21
2015-01-21 929
929








