Пример 5.1 биномиальное распределение

Для непрерывной случайной величины задана функция распределения. Найти математическое ожидание, дисперсию, среднеквадратическое отклонение. Вычислить вероятность того, что отклонение случайной величины от её математического ожидания не более среднеквадратического отклонения.

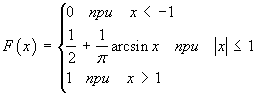
20. Целочисленная случайная величина X имеет биномиальное распределение, если вероятность ее возможных значений вычисляется по формуле Бернулли

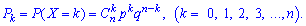
В табличной форме этот закон имеет следующий вид:

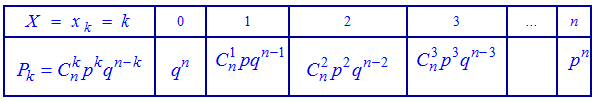
При проверке выполнения условия нормировки используется формула бинома Ньютона, поэтому закон распределения называют биномиальным

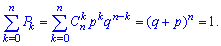
Построим вероятностную образующую функцию для этого закона

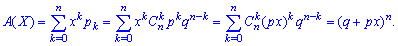
Итак, вероятностная образующая функция для биномиального закона ровна

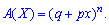
Найдем основные числовые характеристики для этого закона

1. Математическое ожидание случайной величины через образующую функцию для биномиального распределения вычисляем по формуле

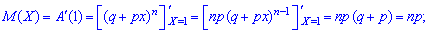
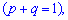
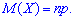
2. Вторая производная от образующей функции для биномиального распределения в единице примет значение

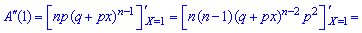
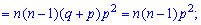
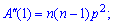
На основе найденного значения можно вычислять дисперсию

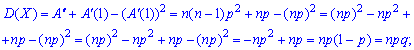
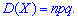
Имея дисперсию нетрудно установить среднее математическое отклонение

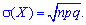
3. Коэффициент асимметрии А(Х) и эксцесс Е(Х) для биномиального распределения определяют по формулам

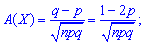
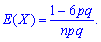
В случае роста количества испытаний n асимметрия и эксцесс стремятся к нулю.

Перейдем к практической стороне биномиального распределения

Задача 1. В партии однотипных деталей стандартные составляют 97%. Наугад из партии берут 400 деталей. Определить математическое ожидание, дисперсию и среднее квадратическое отклонение М(Х), D(X), S(Х) для дискретной случайной величины Х — появления числа стандартных деталей среди 400 наугад взятых.

Решение. Целочисленных случайная величина Х имеет биномиальное закон распределения вероятностей, которая может принимать значения Х = k = 0, 1, 2,..., 400. Вероятности возможных значений для данной задачи определяются по формуле Бернулли и составляют 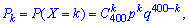где р = 0,97 — вероятность появления стандартной детали, q = 1 – p =1 – 0,97 = 0,03 — вероятность появления нестандартной детали. Согласно приведенным выше формулам определяем нужные величины:

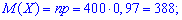
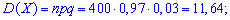
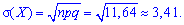
21. Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

Распределение Пуассона играет ключевую роль в теории массового обслуживания.

Определение

Выберем фиксированное число 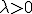и определим дискретное распределение, задаваемое следующей функцией вероятности:

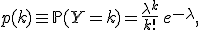
где

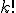обозначает факториал,

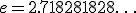— основание натурального логарифма.

Тот факт, что случайная величина 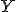имеет распределение Пуассона с параметром 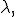записывается: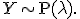

Моменты

Производящая функция моментов распределения Пуассона имеет вид:

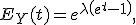
откуда

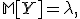
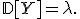
Для факториальных моментов распределения справедлива общая формула:

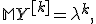
где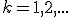

А так как моменты и факториальные моменты линейным образом связаны, то часто для Пуассоновского распределения исследуются именно факториальные моменты, из которых при необходимости можно вывести и обычные моменты.

Свойства распределения Пуассона

Сумма независимых пуассоновских случайных величин также имеет распределение Пуассона. Пусть 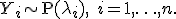Тогда

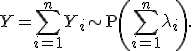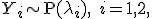Пусть и 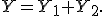Тогда условное распределение 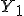при условии, что 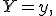биномиально. Более точно:

23. ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЕ

непрерывное распределение вероятностей случайной величины X, задаваемое плотностью

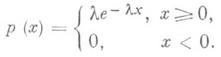(1)

Плотность р(х).зависит от положительного масштабного параметра l. Формула для моментов: , в частности - для математич. ожидания 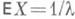и дисперсии 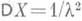; характеристич. функция: (1- it/ l) ^-1.

П. р. входит в семейство распределений, называемых гамма-распределениями и задаваемых плотностью

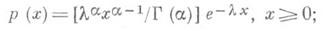
n-кратная свертка распределения (1) равна гамма-распределению с тем же самым параметром lи с a =п. П. р.- единственное распределение, обладающее свойством отсутствия последействия: для любых х>0, у >0 выполняется равенство

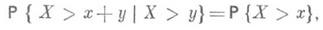(2)

где Р{ Х>х+у|Х>у } - условная вероятность события X>x+y при условии X>y. Свойство (2) называется также марковским свойством.

В однородном пуассоновском процессе расстояние между двумя последовательными скачками траектории имеет П. р. Наоборот, процесс восстановления с показательным временем жизни (1) является пуассоновским процессом восстановления. П. р. часто возникает как предельное при суперпозиции или разрежении процессов восстановления, в задачах пересечения высокого уровня в различных схемах блуждания, в критических ветвящихся процессах и т. п.

Упомянутыми выше свойствами объясняется широкое применение П. р. при расчетах различных систем в теории массового обслуживания и в теории надежности. Предполагая времена занятости приборов случайными, независимыми друг от друга и распределенными показательно, можно благодаря свойству (2) изучать системы массового обслуживания с помощью конечных или счетных цепей Маркова с непрерывным временем. Аналогичным образом используются цепи Маркова и в теории надежности, где времена исправной работы отдельных приборов часто можно предполагать независимыми и распределенными показательно.

24.

Нормальное распределение — одно из важнейших распределений в теории вероятностей; термин принадлежит Карлу Пирсону (K.Pearson); встречаются также названия: второй закон Лапласа, закон Гаусса, лапласовское распределение, гауссовское распределение, распределение Лапласа-Гаусса, распределение Гаусса-Лапласа; применяется как по отношению к распределениям вероятностей случайных величин, так и по отношению к совместным распределениям вероятностей нескольких случайных величин — к многомерным распределениям случайных векторов; общее определение нормального распределения обычно сводится к одномерному случаю.

Распределение вероятностей случайной величины ξ называется нормальным, если оно имеет плотность вероятности вида

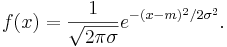
Семейство нормальных распределений зависит от двух параметров m и σ > 0, где

— математическое ожидание, а

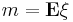
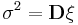
— дисперсия нормальной случайной величины.

\emph {Характеристическая функция} одномерной нормальной случайной величины имеет вид

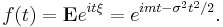
Кривая нормальной плотности y = f (x) симметрична относительно ординаты, проходящей через точку x = m, и имеет в этой точке единственный максимум, равный 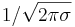. Изменение σ меняет форму кривой: с уменьшением σ кривая нормальной плотности становится более островершинной; изменение m при постоянном σ вызывает смещение кривой вдоль оси абсцисс, не меняя формы кривой. Площадь, заключённая под кривой нормальной плотности всегда равна единице.

При m = 0, σ = 1 распределение называется стандартным нормальным распределением и соответствующая функция распределения принимает вид

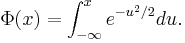
В общем (настандартном) случае нормальная функция распределения вычисляется через стандартную по формуле

F (x; m,σ) = Φ((x − m) / σ).

Функция стандартного нормального распределения (и несколько её производных) затабулированы.

Для нормального распределения

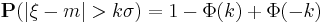
— вероятность данного неравенства убывает достаточно быстро с ростом k. Во многих приложениях обычно пренебрегают возможностью отклонений от m больше, чем на 3σ, пользуясь так называемым правилом трёх сигм (вероятность выхода за три сигмы меньше 0.003, см. таблицу ниже).

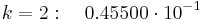
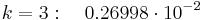
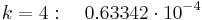
Нормальное распределение встречается во впечатляюще большом числе приложений. Теоретическое объяснение этого факта дают предельные теоремы теории вероятностей, из которых следует, что нормальное распределение служит хорошим приближением каждый раз, когда исследуемая случайная величина представляет собой сумму большого числа независимых случайных величин, максимальная из которых мала по сравнению со всей суммой

25. При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм. Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:

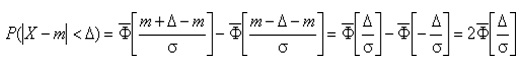
Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:

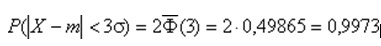
Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее. На практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.

Преобразуем формулу

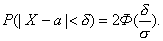
Введем обозначение

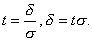
Тогда получим:

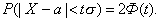
Если t=3, то

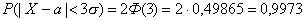
т. е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973.

Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027=1-0,9973. Это означает, что лишь в 0,27% случаев так может произойти. Такие события, исходя из принципа невозможности маловероятных событий можно считать практически невозможными. В этом и состоит сущность правила трех сигм:

Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математиче­ского ожидания не превосходит утроенного среднего квадратического отклонения.

На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.