Если функция распределения случайной величины 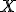 имеет вид:
имеет вид:
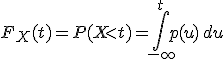 , где
, где 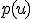 - интегрируемая неотрицательная функция,
- интегрируемая неотрицательная функция,
тогда эта случайная величина называется абсолютно непрерывной. Функция 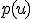 при этом называется плотностью распределения. Плотность распределения удовлетворяет свойствам:
при этом называется плотностью распределения. Плотность распределения удовлетворяет свойствам:
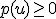 и
и 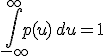 .
.
И наоборот, любая интегрируемая функция 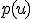 , удовлетворяющая этим свойствам, может быть взята в качестве плотности распределения некоторой случайной величины.
, удовлетворяющая этим свойствам, может быть взята в качестве плотности распределения некоторой случайной величины.
Поскольку функция распределения является функцией верхнего предела от плотности, то последняя восстанавливается по ней дифференцированием: 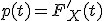 .
.
15.
Таблица
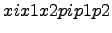
называется законом распределения дискретной случайной величины 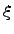 .
.
Для наглядности закон распределения дискретной случайной величины изображают графически, для чего в прямоугольной системе координат строят точки 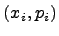 и соединяют последовательно отрезками прямых. Получающаяся при этом ломаная линия называется многоугольником распределения случайной величины
и соединяют последовательно отрезками прямых. Получающаяся при этом ломаная линия называется многоугольником распределения случайной величины 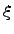 .
.
Если возможными значениями дискретной случайной величины 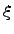 являются 0, 1, 2, …, n, а соответствующие им вероятности вычисляются по формуле Бернулли:
являются 0, 1, 2, …, n, а соответствующие им вероятности вычисляются по формуле Бернулли:
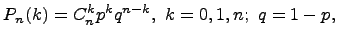
то говорят, что случайная величина 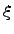 имеет биномиальный закон распределения:
имеет биномиальный закон распределения:
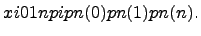
Пусть заданы натуральные числа m, n, s, причем 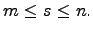 Если возможными значениями дискретной случайной величины
Если возможными значениями дискретной случайной величины 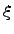 являются 0,1,2,…, m, а соответствующие им вероятности выражаются по формуле
являются 0,1,2,…, m, а соответствующие им вероятности выражаются по формуле
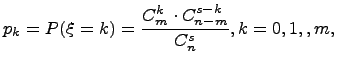
то говорят, что случайная величина 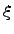 имеет гипергеометрический закон распределения.
имеет гипергеометрический закон распределения.
Другими часто встречающимися примерами законов распределения дискретной случайной величины являются:
геометрический
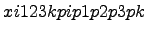
где 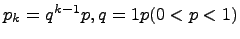 ;
;
Закон распределения Пуассона:
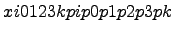
где
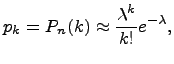
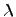 - положительное постоянное.
- положительное постоянное.
Закон распределения Пуассона является предельным для биномиального при 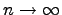 ,
, 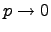 ,
, 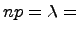 . Виду этого обстоятельства при больших n и малых p биномиальные вероятности вычисляются приближенно по формуле Пуассона:
. Виду этого обстоятельства при больших n и малых p биномиальные вероятности вычисляются приближенно по формуле Пуассона:
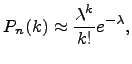
 2015-01-21
2015-01-21 4020
4020
