2015-01-21
1197
1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей: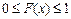 
.
☺ Утверждение следует из того, что функция распределения – это вероятность. ☻
- Функция распределения случайной величины есть неубывающая функция на всей числовой оси.
☺ Пусть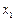 
и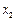 
- точки числовой оси, причем 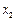> 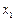. Покажем, что 
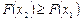. Рассмотрим 2 несовместных события 
, 
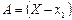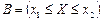. Тогда 
.
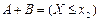Это соотношение между событиями легко усматривается из их геометрической интерпретации (рис.3.6). По теореме сложения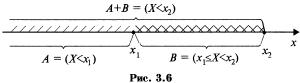 
:
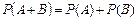или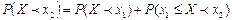 
откуда 
.
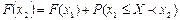Так как вероятность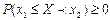 
, то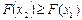 
, т.е. 
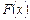- неубывающая функция. ☻
- На минус бесконечности функция распределения равна нулю, на плюс бесконечности равна единице, т.е.
.
☺ 
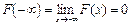
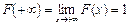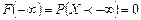как вероятность невозможного события 
.
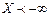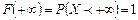как вероятность достоверного события 
. ☻
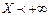4. Вероятность попадания случайной величины в интервал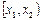 
(включая 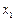) равна при ращению ее функции распределения на этом интервале, т.е.:
.
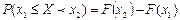☺ Формула следует непосредственно из формулы . ☻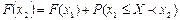
17. Непрерывная случайная величина (НОВ). Вероятность отдельно взятого значения НСВ. Математическое ожидание и дисперсия нсв.
| Определение. Случайная величина Х называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек (точки излома). |
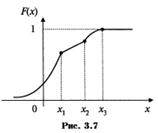На рис. 3.7 показана Функция распределения непрерывной случайной величины Х, дифференцируемая во всех точках, кроме трех точек излома.
Теорема. Вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю.
☺ Покажем, что для любого значения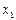 
случайной величины Х вероятность 
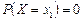. Представим 
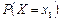в виде 
.
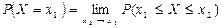Применяя свойство 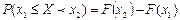функции распределения случайной величины Х и учитывая непрерывность F(x), получим:
. ☻
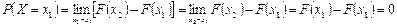Из приведенной выше теоремы следует, что нулевой вероятностью могут обладать и возможные события, так как событие, состоящее в том, что случайная величина Х приняла конкретное значение 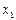, является возможным.
Следствие. Если Х - непрерывная случайная величина, то вероятность попадания случайной величины в интервал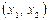 
не зависит от того, является этот интервал открытым или закрытым, т.е.
.
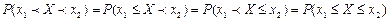Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл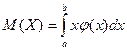 
. Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле: 
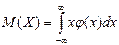. При этом предполагается, что интеграл абсолютно сходится.
Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения.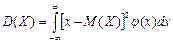 
.
По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула: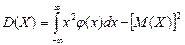 
.
18. Плотность вероятности непрерывной случайной величины, ее определение, свойства и график.
Определение. Плотностью вероятности (плотностью распределения или просто плотностью) 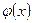 непрерывной случайной величины Х называется производная ее функции распределения  |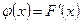
Про случайную величину Х говорят, что она имеет распределение (распределена) с плотностью 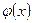на определенном участке оси абсцисс. Плотность вероятности 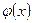, как и функция распределения F(x), является одной из форм закона распределения, но в отличие от функции распределения она существует только для непрерывныхслучайных величин. Плотность вероятности иногда называют дифференциальной функцией или дифференциальным законом распределения. График плотности вероятности 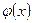называется кривой распределения.
