Замечательные пределы

1) первым замечательным пределом называется следующий предел

Lim sinx/x =1

Xстремится к 0

Доказательство геометрия-нереально написать

2. Второй замечательный предел

Рассмотрим числовую последовательность

Xn=(1+1/n)^n

X1=(1+1/1)’=2

X2=(1+1/2)’2=2.25

Рисуем координатную прямую

Можно доказать, что последовательность ограничена числом 3

Последовательность – возрастающая и ограниченная сверху

Последовательность имеет предел

е = lim (1+1/n)^n

nстремится к бесконечности

Можно показать, что функция

y= (1+1/x)^x при x стремящемся к бесконечности (где х в отличие от натурального числа и «пробегает» все значения числовой оси –не только целые) имеет предел, равный числу е

Lim (1+1/x)^x=e

Xстремится к бесконечности

Другой вид второго замечательного предела

y = 1/x; x=1/y, при х стремящемся к бесконечности, y стремящемся к 0

В результате получается еще одна запись числа е

Lim (1+y)^1/y=e

y стремится к 0

13) неопределенностями.

выражений, значение которых не определено. Такие выражения называют неопределенностями.

Перечислим все основные виды неопределенностей: ноль делить на ноль (0 на 0), бесконечность делить на бесконечность , ноль умножить на бесконечность , бесконечность минус бесконечность , единица в степени бесконечность , ноль в степени ноль 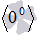, бесконечность в степени ноль .

ВСЕ ДРУГИЕ ВЫРАЖЕНИЯ НЕОПРЕДЕЛЕННОСТЯМИ НЕ ЯВЛЯЮТСЯ И ПРИНИМАЮТ ВПОЛНЕ КОНКРЕТНОЕ КОНЕЧНОЕ ИЛИ БЕСКОНЕЧНОЕ ЗНАЧЕНИЕ.

Раскрывать неопределенности позволяет:

· упрощение вида функции (преобразование выражения с использованием формул сокращенного умножения, тригонометрических формул, домножением на сопряженные выражения с последующим сокращением и т.п.);

· использование замечательных пределов;

· применение правила Лопиталя;

· использование замены бесконечно малого выражения ему эквивалентным

·

• Если m равно n, то предел равен отношению коэффициентов при старших степенях;
• Если m больше n, то предел равен бесконечности;
• Если m меньше n, то предел равен 0.

14) Функция f(x) непрерывна в точке X0 если она:

- определена в точке Х0 то есть существует f(x0)

- имеет конечный предел при х=>0

- предел равен значению функции в точке х0

Приращение аргумента – разность между двумя значениями аргумента («новым» и «старым»). Обычно обозначается через D х: D х = x ₁ – x ₀

Приращение функции – разность между двумя значениями функции.

1. Функция одной переменной. Пусть задана функция у = f(x), определенная при значении аргумента, равном х ₀. Дадим аргументу приращение D х, т.е. рассмотрим значение аргумента, равное x ₀ + D х. Предположим, что это значение аргумента также входит в область определения данной функции. Тогда разность
D y = f(x ₀ + D х) – f(x₀) называется приращением функции.

2. Функция многих переменных. Пусть в некоторой области D n -мерного пространства задана функция z = f (x ₁; x ₂; …; x _n) и пусть точки М и N принадлежат области D – входят в область определения данной функции. При переходе из точки M в точку N каждая координата х _i точки получит приращение D х _i, i = 1, 2, …, n, а данная функция – приращение D z = f (N) – f (M) = f (x ₁+D x ₁; x ₂+D x ₂; …; x _n+D x _n) – f (x ₁; x ₂; …; x _n). Это приращение называют иногда полным, в отличие от частного приращения D_i z, при котором получает приращение только аргумент х _i, а все остальные аргументы сохраняют первоначальное значение:D_i z = f (x ₁, x ₂, …; x _i–1; x _i+1; …; x _n) – f (x ₁; x ₂; …; x _n).