Пусть функция 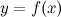 зависит от переменной
зависит от переменной  и дифференцируема в точке
и дифференцируема в точке  . Может оказаться, что в точке
. Может оказаться, что в точке  дифференциал
дифференциал 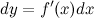 , рассматриваемый как функция от
, рассматриваемый как функция от  , есть также дифференцируемая функция. Тогда существует дифференциал от дифференциала
, есть также дифференцируемая функция. Тогда существует дифференциал от дифференциала 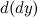 данной функции, который называется дифференциалом второго порядка функции
данной функции, который называется дифференциалом второго порядка функции 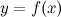 . Дифференциал второго порядка обозначается следующим образом:
. Дифференциал второго порядка обозначается следующим образом:
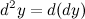
Аналогично определяются дифференциалы более высоких порядков.
Определение
Дифференциалом 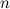 -го порядка
-го порядка 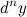 функции
функции 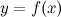 называется дифференциал от дифференциала
называется дифференциал от дифференциала 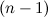 -го порядка этой функции, то есть
-го порядка этой функции, то есть
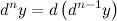
Получим формулы, выражающие дифференциалы высших порядков. Рассмотрим несколько случаев.
Случай независимой переменной
Пусть 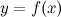 - функция независимой переменной
- функция независимой переменной  , имеющая дифференциалы любого порядка. Первый дифференциал функции
, имеющая дифференциалы любого порядка. Первый дифференциал функции
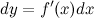
где 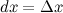 - некоторое приращение независимой переменной
- некоторое приращение независимой переменной  , которое мы задаем сами и которое не зависит от
, которое мы задаем сами и которое не зависит от  . По определению
. По определению
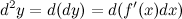
Переменной является аргумент  . Значит, для дифференциала величина
. Значит, для дифференциала величина 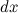 является постоянной и поэтому может быть вынесена за знак дифференциала. То есть дифференциал второго порядка
является постоянной и поэтому может быть вынесена за знак дифференциала. То есть дифференциал второго порядка
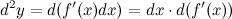
Для вычисления дифференциала 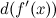 применим формулу дифференциала первого порядка к функции
применим формулу дифференциала первого порядка к функции 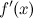 . Тогда получим:
. Тогда получим:
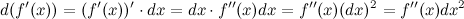
Итак,
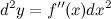
Рассматривая последовательно дифференциалы все более высокого порядка, получим формулу дифференциала 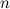 -го порядка:
-го порядка:
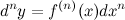
4) Применение дифференциала в приближенных вычислениях
Приращение 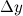 функции
функции 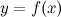 представимо в виде:
представимо в виде:
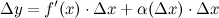
где функция 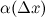 является б.м. функцией при стремлении аргумента
является б.м. функцией при стремлении аргумента 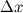 к нулю. Так как
к нулю. Так как 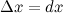 , то
, то
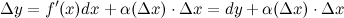
В силу того, что второе слагаемое 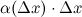 является бесконечно малым, то им можно пренебречь, а поэтому
является бесконечно малым, то им можно пренебречь, а поэтому
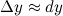
А так как в нахождении дифференциал значительно проще, чем приращение функции, то данная формула активно используется на практике.
Для приближенного вычисления значения функции применяется следующая формула:
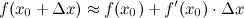
25)Теорема Ферма. Если дифференцируемая на промежутке Х функция y=f(x) достигает наибольшего или наименьшего значения во внутренней точке х0 этого промежутка, то производная функции в этой точке равна 0.
По условию, ф-ия имеет производную в точке х0, сл-но, при дельта х<0 предел дельта y/дельта х <=> f,(х0)=0
Геометрический смысл теоремы Ферма:
В точке наиб и наим значения, достигаемого внутри промежутка х, касательная к графику ф-ии параллельна оси Ох
 2015-01-21
2015-01-21 836
836








