2015-01-21
2445
Непрерывная случайная величина Х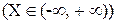 
называется распределенной по нормальному закону (или закону Гаусса), если ее плотность распределения 
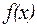имеет вид
,
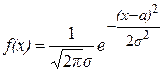где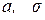 
– численные параметры нормального закона распределения, 
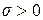. График плотности распределения 
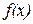в этом случае называется нормальной кривой (или кривой Гаусса).
Нормальная кривая расположена выше оси абсцисс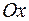 
, симметрична относительно вертикальной прямой (
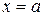), имеет своей горизонтальной асимптотой ось абсцисс, имеет две точки перегиба (
; 
), (
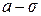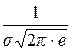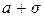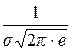; ) и достигает максимума при 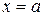, равного 
.
 |
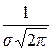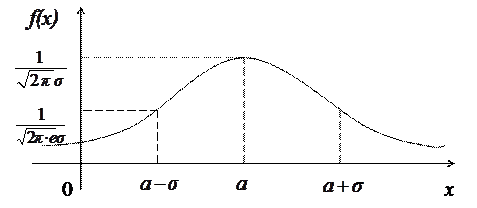Рисунок 11 - Кривая Гаусса
Параметры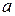 
и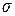 
нормального распределения имеют следующий вероятностный смысл:
· параметр 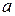равен математическому ожиданию нормально распределенной случайной величины Х, т.е. 
;
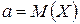· параметр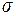 
равен среднему квадратическому отклонению нормально распределенной случайной величины Х, т.е. 
.
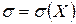Отметим также, что для нормального закона распределения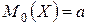 
, 
.
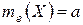Распределение Пирсона "хи-квадрат"
Рассмотрим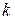 
независимых нормально распределенных случайных величин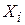 
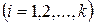с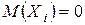 
, 
, 
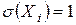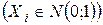и составим сумму квадратов этих величин:
= 
.
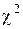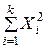Определенная таким образом случайная величина 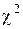называется распределенной по закону "хи-квадрат" (закону Пирсона) с 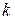степенями свободы.
Заметим, что распределение "хи-квадрат" имеет один параметр 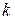– число степеней свободы. При увеличении числа степеней свободы распределение 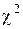медленно приближается к нормальному.
Распределение Стьюдента (t-распределение)
Рассмотрим две независимые случайные величины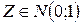 
и V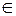 
(
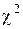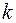); т.е. случайная величина Z имеет нормальное распределение с 
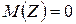и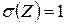 
, а независимая от нее случайная величина V распределена по закону 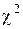с с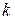тепенями свободы. Составим случайную величину
.
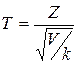Определенная таким образом случайная величина T называется распределенной по закону Стьюдента с 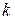степенями свободы.
Отметим, что распределение Стьюдента имеет один параметр 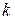– число степеней свободы. При увеличении числа степеней свободы распределение Стьюдента быстро приближается к нормальному.
Распределение Фишера (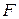
-распределение)
Рассмотрим две независимые случайные величины U и V, распределенные по закону 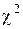со степенями свободы 
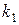и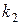 
соответственно. Составим случайную величину
.
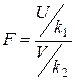Определенная таким образом случайная величина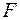 
называется распределенной по закону Фишера со степенями свободы 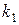и .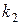
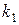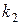Заметим, что распределение Фишера имеет два параметра и – числа степеней свободы.
Отметим также, что имеются специальные таблицы квантилей распределений N (0,1), (),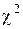 
(), 
.
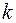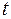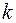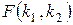Биноминальное распределение
Рассмотрим дискретную случайную величину Х, имеющую смысл числа появлений некоторого события А в серии из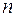 
независимых опытов по схеме Бернулли. Возможные значения случайной величины Х, очевидно, таковы: 0, 1, 2, …, 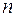. Для нахождения вероятностей этих возможных значений достаточно воспользоваться формулой Бернулли:
(
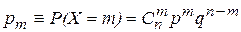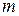=0, 1, …, ),
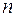где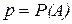 
– вероятность появления события А в одном опыте; 
.
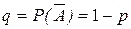Данная формула и является аналитическим выражением биноминального закона распределения дискретной случайной величины.
Рассмотрим дискретную случайную величину Х, возможные значения которой составляют множество всех целых неотрицательных чисел: 0, 1, 2, …, 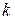, …, причем последовательность этих значений теоретически не ограничена (бесконечна). Вероятности этих возможных значений зададим следующей формулой:
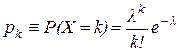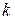( =0, 1, 2, …),
где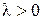 
– некоторая положительная величина, называемая параметром распределения.
Данная формула является аналитическим выражением закона распределения Пуассона.
Отметим, что закон Пуассона приближенно заменяет биноминальный закон распределения в случаях, когда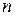 
велико, а 
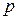мало; при этом параметр 
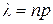. По этой причине закон распределения Пуассона часто называют законом редких (
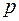мало) массовых ( велико) явлений.
