Основные теоремы

1. Необходимый признак сходимости числового ряда

Теорема. Если ряд (1) сходится, то его общий член a_n стремится к нулю, т.е. .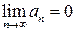

Следствие. Если общий член a_n ряда (1) не стремится к нулю, то данный ряд расходится.

2. Критерий сходимости ряда

Теорема. Для того, чтобы сходился ряд (1) необходимо и достаточно, чтобы сходился его k - ый остаточный ряд (2).

3. Признаки сравнения положительных рядов.

Теорема 1. Пусть даны два ряда с положительными членами:

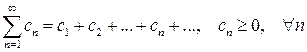, (6)

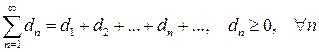(7)

и пусть, начиная с некоторого номера n, выполняется неравенство:

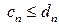, (8)

Тогда:

1) из сходимости ряда (7) следует сходимость ряда (6);

2) из расходимости ряда (6) следует расходимость ряда (7).

Теорема 2. Если для рядов (6) и (7) существует предел

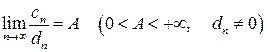, (9)

то ряды (6) и (7) ведут себя одинаково, т. е. либо сходятся, либо расходятся одновременно.

4. Признаки сходимости положительных рядов

Теорема 1 ( Признак Даламбера). Пусть задан положительный ряд (6), члены которого отличны от 0, и существует предел

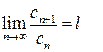(10)

Тогда:

1) Если l< 1, то ряд (6) сходится;

2) Если l> 1, то ряд (6) расходится;

3) Если l= 1, то теорема не дает ответа на вопрос о поведении ряда (6).

Теорема 2 (признак Коши). Пусть задан положительный ряд (6) и существует предел

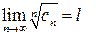(11)

Тогда:

1) Если l< 1, то ряд (6) сходится;

2) Если l> 1, то ряд (6) расходится;

3) Если l= 1, то теорема не дает ответ на вопрос о поведении ряда (6).

Теорема 3. (Интегральный признак Коши). Пусть члены положительного ряда (6) не возрастают, т.е. 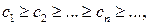и пусть f (x)- функция, заданная на промежутке 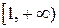, положительная, непрерывная и невозрастающая функция на этом промежутке, такая, что

f (1)= c ₁, f (2)= c ₂, …, f (n) =c_n, ….

Тогда:

1) Если несобственный интеграл

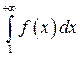(12)

сходится, то и ряд (6) сходится;

2) Если несобственный интеграл (12) расходится, то расходится и ряд (6).