Задание 1. Найти площадь фигуры, ограниченной данными линиями. Сделать чертеж.
1. 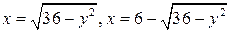 .
.
2. 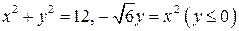 .
.
3. 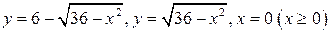 .
.
4. 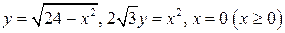 .
.
5. 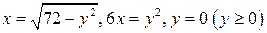 .
.
6. 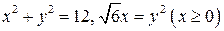 .
.
7. 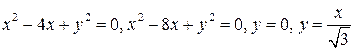 .
.
8. 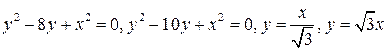 .
.
9. 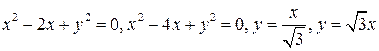 .
.
10. 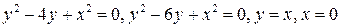 .
.
Задание 2. Найти объем тела, ограниченного данными поверхностями. Сделать чертежи данного тела и его проекции на плоскость Oxy.
1. 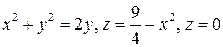 .
.
2. 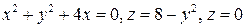 .
.
3. 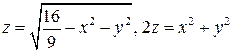 .
.
4. 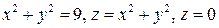 .
.
5. 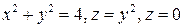 .
.
6. 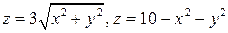 .
.
7. 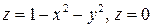 .
.
 8.
8. 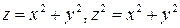 .
.
9. 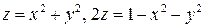 .
.
10. 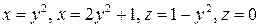 .
.
Задание 3. Вычислить криволинейные интегралы 2-го рода, взятые вдоль данных кривых.
1. 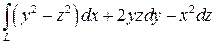 , где L - кривая x = t, y = t 2, z = t 3,
, где L - кривая x = t, y = t 2, z = t 3, 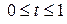 .
.
2. 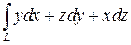 , где L - виток винтовой линии x= cos t, y= sin t, z=t,
, где L - виток винтовой линии x= cos t, y= sin t, z=t, 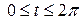 .
.
3. 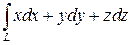 , где L - виток конической винтовой линии x=et cos t, y=et sin t, z=et от точки А (0,0,0) до точки В (1,0,1).
, где L - виток конической винтовой линии x=et cos t, y=et sin t, z=et от точки А (0,0,0) до точки В (1,0,1).
4. 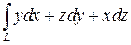 , где L - отрезок прямой ОС от точки О (0,0,0) до точки С (1,1,1).
, где L - отрезок прямой ОС от точки О (0,0,0) до точки С (1,1,1).
5. 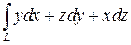 , где L - ломанная ОАВС, соединяющая точки О (0,0,0), А (1,0,0), В (1,1,0), С (1,1,1)
, где L - ломанная ОАВС, соединяющая точки О (0,0,0), А (1,0,0), В (1,1,0), С (1,1,1)
6. 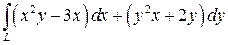 , где L - верхняя половина эллипса x= 5cos t, y= 4sin t,
, где L - верхняя половина эллипса x= 5cos t, y= 4sin t, 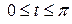 .
.
7. 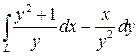 , где L - отрезок прямой АВ от точки А (1,2) до точки В (3,6).
, где L - отрезок прямой АВ от точки А (1,2) до точки В (3,6).
8. 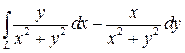 , где L - граница треугольника АВС с вершинами А (2,0), В (2,2), С (0,2).
, где L - граница треугольника АВС с вершинами А (2,0), В (2,2), С (0,2).
9. 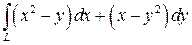 , где L - дуга окружности x= 3cos t, y= 3sin t, от точки А (3,0) до точки В (0,3).
, где L - дуга окружности x= 3cos t, y= 3sin t, от точки А (3,0) до точки В (0,3).
10. 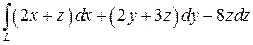 , где L - виток винтовой линии x= 3cos t, y= 3sin t, z= 4 t,
, где L - виток винтовой линии x= 3cos t, y= 3sin t, z= 4 t, 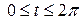 .
.
Задание 4. Вычислить следующие поверхностные интегралы 1-го рода. Сделать чертежи данной поверхности и ее проекции на плоскость Oxy.
1. 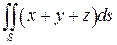 , где S - поверхность
, где S - поверхность 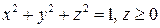 .
.
2. 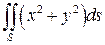 , где S - граница тела
, где S - граница тела 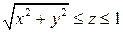 .
.
3. 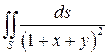 , где S - граница тетраэдра
, где S - граница тетраэдра 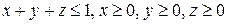 .
.
4. 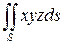 , где S - поверхность
, где S - поверхность 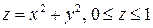 .
.
5. 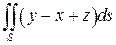 , где S - плоскость 2 x-y+ 2 z- 2=0, расположенная в 1-ом октанте.
, где S - плоскость 2 x-y+ 2 z- 2=0, расположенная в 1-ом октанте.
6. 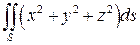 , где S - поверхность сферы
, где S - поверхность сферы 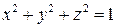 .
.
7. 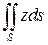 , где S - часть поверхности
, где S - часть поверхности 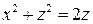 , вырезанная поверхностью
, вырезанная поверхностью 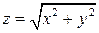 .
.
8. 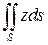 , где S - полусфера
, где S - полусфера 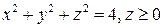 .
.
9. 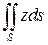 , где S - поверхность конуса
, где S - поверхность конуса 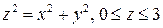 .
.
10. 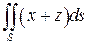 , где S - плоскость
, где S - плоскость 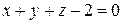 , расположенная в 1-ом октанте.
, расположенная в 1-ом октанте.
Задание 5. Дано векторное поле 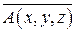 и плоскость P, которая с координатными плоскостями образует пирамиду T. Пусть SABC - основание пирамиды, принадлежащее плоскости P, LABC - контур, ограничивающий SABC. Вычислить:
и плоскость P, которая с координатными плоскостями образует пирамиду T. Пусть SABC - основание пирамиды, принадлежащее плоскости P, LABC - контур, ограничивающий SABC. Вычислить:
1) поток векторного поля 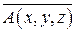 через полную поверхность S пирамиды T в направлении внешней нормали (непосредственно и по теореме Гаусса-Остроградского);
через полную поверхность S пирамиды T в направлении внешней нормали (непосредственно и по теореме Гаусса-Остроградского);
2)циркуляцию данного векторного поля 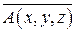 по контуру LABC (непосредственно и по теореме Стокса).
по контуру LABC (непосредственно и по теореме Стокса).
1. 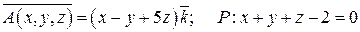 .
.
2. 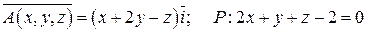 .
.
3. 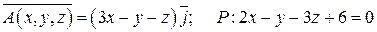 .
.
4. 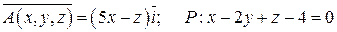 .
.
5. 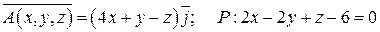 .
.
6. 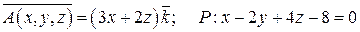 .
.
7. 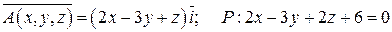 .
.
8. 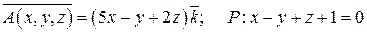 .
.
9. 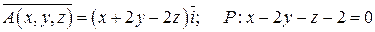 .
.
10. 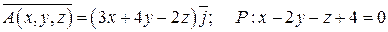 .
.
 2015-01-21
2015-01-21 925
925








