Ряд (1) называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные члены.
Теорема (достаточный признак сходимости знакопеременного ряда). Пусть задан знакопеременный ряд
a 1 + a 2 + … + an + …. (13)
Если ряд, составленный из абсолютных величин членов данного ряда
| a 1| + | a 2| + … + | an | +…, (14)
сходится, то сходится и данный ряд (13).
Ряд (13) называется абсолютно сходящимся, если сходится ряд (14), составленный из абсолютных величин членов ряда (13). Если же знакопеременный ряд (13) сходится, а ряд (14) расходится, то ряд (13) называется условно или неабсолютно сходящимся.
Ряд вида
a 1 – a 2 + a 3 – a 4 +… + 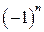 an + …., (15)
an + …., (15)
где 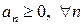 , называется знакочередующимся.
, называется знакочередующимся.
Теорема (признак Лейбница). Знакочередующийся ряд (15) сходится, если абсолютные величины его членов не возрастают, а общий член стремится к нулю, т.е. если выполняются следующие два условия:
1) 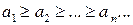 (16)
(16)
2) 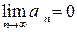 (17)
(17)
Замечание 1. При решении задач на исследование сходимости ряда полезно знать особенности поведения следующих рядов:
1. Ряд, составленный из членов геометрической прогрессии 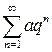 : сходится при
: сходится при 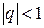 и расходится при
и расходится при 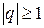 , q – знаменатель прогрессии;
, q – знаменатель прогрессии;
2. Обобщенный гармонический ряд 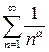 : сходится при
: сходится при 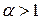 и расходится при
и расходится при 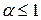 . В частном случае (
. В частном случае (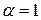 ) получаем гармонический ряд
) получаем гармонический ряд 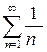 , который расходится.
, который расходится.
Замечание 2. Если ряд (15) удовлетворяет условиям признака Лейбница, то ошибка, совершаемая при замене S на Sn, не превосходит по абсолютной величине первого из отброшенных членов. Это свойство используется для приближенных вычислений.
Задание 1. Исследовать на сходимость ряд 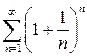 .
.
Решение. Так как 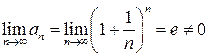 (второй замечательный предел), то в силу следствия из необходимого признака сходимости ряда получаем, что данный ряд расходится.
(второй замечательный предел), то в силу следствия из необходимого признака сходимости ряда получаем, что данный ряд расходится.
Задание 2. Исследовать на сходимость ряд 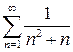 .
.
Решение. Выясним поведение данного ряда с помощью признака сравнения. Для этого сравним его с рядом 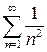 (это – обобщенный гармонический ряд, который сходится, так как
(это – обобщенный гармонический ряд, который сходится, так как 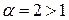 ). Имеем:
). Имеем:
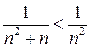
и, следовательно, из сходимости ряда 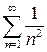 по признаку сравнения следует сходимость и данного ряда.
по признаку сравнения следует сходимость и данного ряда.
Задание 3. Исследовать на сходимость ряд 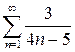 .
.
Решение. Выясним поведение данного ряда с помощью предельного признака сравнения. Сравним данный ряд с рядом 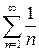 (это - гармонический ряд, который расходится). Имеем:
(это - гармонический ряд, который расходится). Имеем:
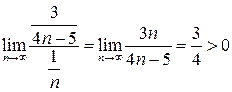
и, следовательно, ряды 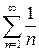 и данный ведут себя одинаково. Таким образом, по предельному признаку сравнения исследуемый ряд расходится.
и данный ведут себя одинаково. Таким образом, по предельному признаку сравнения исследуемый ряд расходится.
Задание 4. Исследовать на сходимость ряд 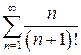 .
.
Решение. Применим к данному ряду признак Даламбера. Имеем:
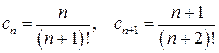 и
и 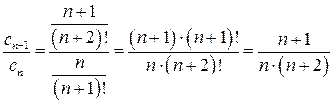
Тогда 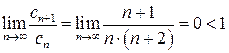 . Следовательно, по признаку Даламбера данный ряд сходится.
. Следовательно, по признаку Даламбера данный ряд сходится.
Задание 5. Исследовать на сходимость ряд 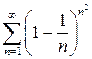 .
.
Решение. Применим к данному ряду признак Коши. Имеем:
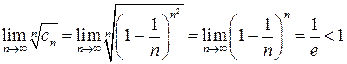 ,
,
и, следовательно, в силу признака Коши данный ряд сходится.
Задание 6. Исследовать на сходимость ряд 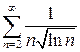 .
.
Решение. Применим к данному ряду интегральный признак Коши. Имеем:
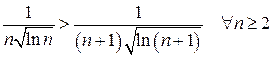 ,
,
что означает, что члены данного ряда убывают. В качестве функции f (x)возьмем функцию 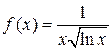 ,
, 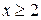 . Эта функция положительная, непрерывная и убывает в области определения, причем
. Эта функция положительная, непрерывная и убывает в области определения, причем 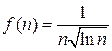 . Рассмотрим несобственный интеграл
. Рассмотрим несобственный интеграл
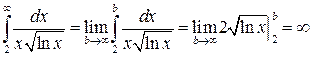
Следовательно, несобственный интеграл расходится. Тогда в силу интегрального признака Коши расходится и данный ряд.
Задание 7. Исследовать на сходимость ряд 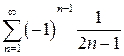 .
.
Решение. Данный ряд является знакочередующимся. Ряд, составленный из абсолютных величин 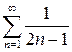 эквивалентен ряду
эквивалентен ряду 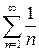 . Последний ряд расходится, следовательно, расходится и ряд, составленный из абсолютных величин исходного ряда. Таким образом, если исходный ряд и сходится, то только условно.
. Последний ряд расходится, следовательно, расходится и ряд, составленный из абсолютных величин исходного ряда. Таким образом, если исходный ряд и сходится, то только условно.
Для исследования исходного ряда на условную сходимость применим к нему признак Лейбница. Имеем:
1) 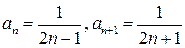 и очевидно, что
и очевидно, что 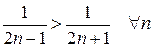
2) 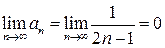
Следовательно, условия признака Лейбница выполнены. Таким образом, исходный ряд сходится условно.
 2015-01-21
2015-01-21 2717
2717








