Одним из методов решения неравенств, содержащих знак модуля, является метод промежутков, который был рассмотрен при решении уравнений с модулем.
Разобъем числовую ось точками, в которых обращаются в нуль выражения, стоящие под знаком модуля.
Выбирая на этих промежутках контрольные точки, проверяем, удовлетворяется ли на них заданное неравенство или нет. Ответом к задаче служит объединение промежутков, где выполняется данное неравенство.
 Пример. Решить неравенство:
Пример. Решить неравенство:
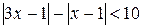 .
.
Решение. Разобъем числовую ось точками 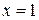 и на промежутки
и на промежутки 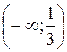 ,
, 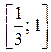 и
и 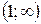 .
.
Рассмотрим промежуток 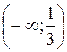 . Взяв контрольную точку, например,
. Взяв контрольную точку, например, 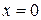 , убеждаемся, что
, убеждаемся, что 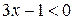 и
и 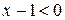 , заменяя модули, получаем равносильное неравенство:
, заменяя модули, получаем равносильное неравенство:
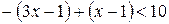 .
.
После элементарных упрощений получаем 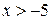 . Значит, решением неравенства на рассматриваемом промежутке является множество
. Значит, решением неравенства на рассматриваемом промежутке является множество 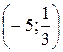 .
.
Перейдем на следующий промежуток 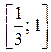 . Взяв контрольную точку
. Взяв контрольную точку 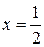 , убеждаемся, что
, убеждаемся, что 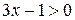 и
и 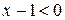 . Неравенство упрощается:
. Неравенство упрощается:
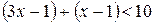 ,
, 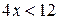 ,
, 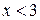 .
.
Решением неравенства является множество 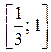 .
.
Перейдем к последнему промежутку 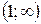 . Убедимся, что на нем
. Убедимся, что на нем 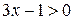 и
и 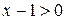 . Неравенство равносильно следующему:
. Неравенство равносильно следующему:
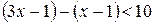 ,
, 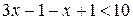 ,
, 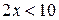 ,
, 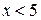 .
.
Получили решение 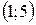 . Осталось объединить решения, полученные в трех случаях:
. Осталось объединить решения, полученные в трех случаях: 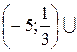
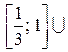
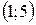 =
= 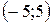 .
.
 2015-01-21
2015-01-21 723
723








