Рассмотрим решение иррациональных неравенств, т.е. неравенств, в которых неизвестная содержится под знаком радикала. Простейшие из них имеют вид:
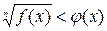 или
или 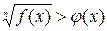 .
.
При рассмотрении этих неравенств будут применяться следующие утверждения:
1. Неравенство вида 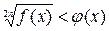 (при натуральном
(при натуральном 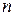 ) равносильно системе неравенств:
) равносильно системе неравенств:
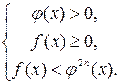
2. Неравенство вида 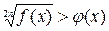 равносильно совокупности двух систем неравенств:
равносильно совокупности двух систем неравенств:
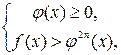 и
и 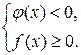
 Пример. Решить неравенство:
Пример. Решить неравенство:
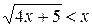 .
.
Решение. Данное неравенство равносильно системе неравенств:

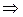
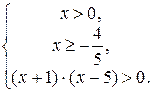

Итак, решением системы является множество 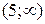 .
.
 Пример. Решить неравенство:
Пример. Решить неравенство:
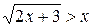 .
.
Решение. Данное неравенство равносильно совокупности систем неравенств:
а) 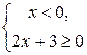 и б)
и б) 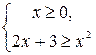
Решением а) системы является множество 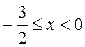 .
.
Решая б) систему, получим:
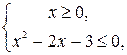
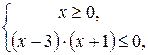

Осталось объединить решения, полученные в обоих случаях: 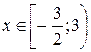
.
 2015-01-21
2015-01-21 1195
1195
