Решить уравнение графически, это когда на одном и том же рисунке построить графики двух функций и найти их точки пересечения, абсциссы этих точек и дадут корни уравнений

Пример. Решить уравнение:

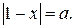
Решение. При 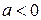уравнение не имеет решения. Рассмотрим случай 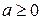и построим графики двух функци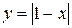й и .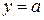

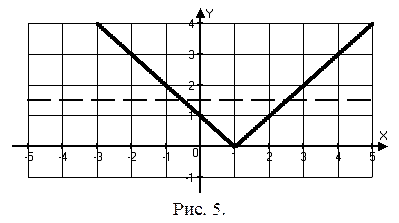
Из графиков видим, что при 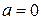, 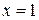уравнение имеет один корень. При 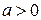графики пересекаются в двух точках, значит уравнение имеет два корня:

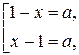
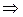
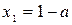и .

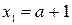Пример. Решить уравнение:

.

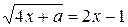Решение. Это уравнение равносильно системе:

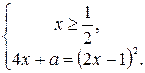
После эквивалентных преобразований получим систему:

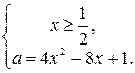
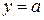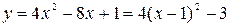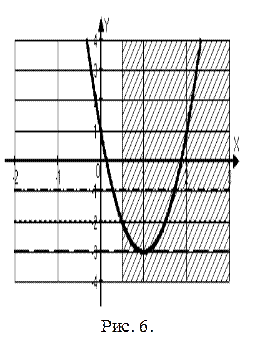
Построим графики функций ; и область значений неравенства 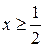(рис. 6).

Есл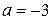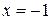и , , при 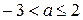уравнение 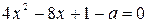имеет два корня:

;

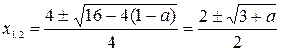при , .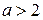

.

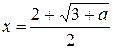Пример. При каких значениях 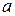все решения неравенства 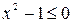являются решениями неравенства .

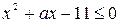Решение. Решим графически. Построим графики функци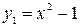й:

и .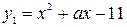

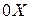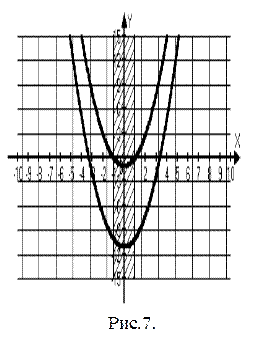
График второй функции пересекает ось в точках: 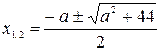. По условию задачи требуется, чтобы все решения первого неравенства являлись решениями второго, значит графики должны быть расположены так, как изображены на рис. 7. Тогда должны выполняться следующие условия:

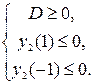
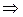
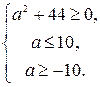
Итак, при 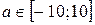решения первого неравенства являются решениями второго.