1.  Сколько надо взять членов арифметической прогрессии:
Сколько надо взять членов арифметической прогрессии:
 =
= 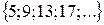 ,
,
чтобы получить сумму, равную 10877?
Решение. По условию 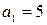 ,
, 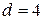 . Подставляя эти значения во вторую формулу суммы арифметической прогрессии:
. Подставляя эти значения во вторую формулу суммы арифметической прогрессии:
 , т.е.
, т.е. 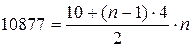 ,
,
после некоторых преобразований, получим уравнение:
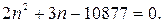
Корни его: 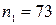 и
и 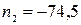 ; из них годится только первый. Следовательно, надо взять 73 члена.
; из них годится только первый. Следовательно, надо взять 73 члена.
2.  Найти арифметическую прогрессию, зная, что сумма первых четырех членов ее равна 26, а произведение тех же членов равно 880.
Найти арифметическую прогрессию, зная, что сумма первых четырех членов ее равна 26, а произведение тех же членов равно 880.
Решение. По условию:
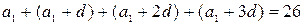 ,
,
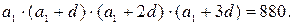
Первое уравнение дает: 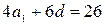 , откуда
, откуда 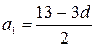 . Подставляя во второе уравнение, и упрощая выражения в скобках, получаем:
. Подставляя во второе уравнение, и упрощая выражения в скобках, получаем:
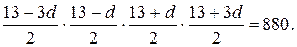
Освобождаясь от знаменателя и перемножая числители (удобно пользоваться формулами сокращенного умножения), приходим к биквадратному уравнению:
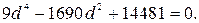
Его корни: 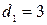 ,
, 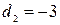 ,
, 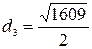 и
и 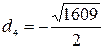 . Из выражения
. Из выражения 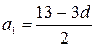 находим соответствующие значения первого члена для четырех арифметических прогрессий:
находим соответствующие значения первого члена для четырех арифметических прогрессий:
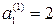 ,
, 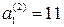 ,
, 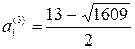 ;
; 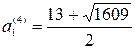 .
.
3.  Найти три числа, составляющих геометрическую прогрессию, если известно, что сумма первого и третьего членов равна 52, а квадрат второго равен 100.
Найти три числа, составляющих геометрическую прогрессию, если известно, что сумма первого и третьего членов равна 52, а квадрат второго равен 100.
Решение. По условию имеем: 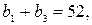
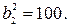
Из второго уравнения имеем: 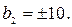 По свойству геометрической прогрессии:
По свойству геометрической прогрессии: 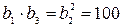 , следовательно, по теореме обратной теореме Виета
, следовательно, по теореме обратной теореме Виета 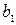 и
и 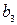 - корни уравнения:
- корни уравнения:
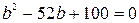 .
.
Отсюда найдем: 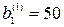 и
и 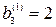 или
или 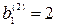 и
и 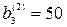 .
.
Ответ: Числа будут: 1) 50; 10; 2 или 2) 50; -10; 2 или 3) 2; 10; 50 или 4) 2; -10; 50.
4.  Доказать, что числа
Доказать, что числа
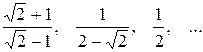
образуют бесконечно убывающую геометрическую прогрессию, и найти предел суммы ее членов.
Решение. Для доказательства того, что данные числа образуют бесконечно убывающую геометрическую прогрессию, надо проверить, будут ли равны отношения: 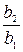 и
и 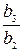 , и будут ли они меньше 1. Имеем:
, и будут ли они меньше 1. Имеем:
1) 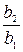 =
= 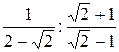 =
= 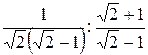 =
= 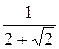 ;
;
2) 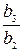 =
= 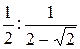 =
= 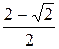 =
= 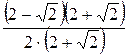 =
= 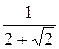 .
.
Так как 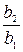 =
= 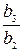 =
= 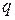 =
= 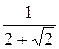
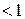 , то данные числа образуют бесконечно убывающую геометрическую прогрессию. По формуле ее суммы находим:
, то данные числа образуют бесконечно убывающую геометрическую прогрессию. По формуле ее суммы находим:
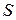 =
= 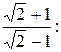
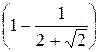 =
= 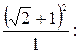
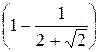 =
= 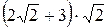 =
= 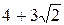 .
.
 2015-01-21
2015-01-21 2959
2959
