2015-01-21
740
1. Уравнения, однородные относительно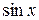 
и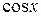 
.
Каждое из уравнений:
,
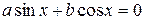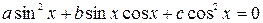и т.д.
называется однородным относительно 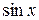и 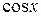. Сумма показателей степеней у 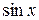и 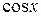во всех членах такого уравнения одинакова. Эта сумма называется степенью однородного уравнения. Делением на 
, 
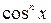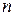степень однородного уравнения, оно приводится к уравнению, алгебраическому относительно 
.
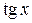Разделив, например, уравнение 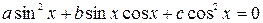на 
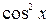, получим уравнение:
.
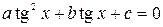При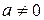 
эти уравнения эквивалентны, так как если 
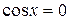, то из первого уравнения получим, что и 
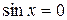, что невозможно ( 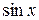и 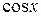при одном и том же аргументе в нуль не обращаются). Далее из эквивалентного уравнения находим 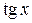, решая квадратное уравнение относительно 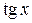, а по значениям 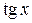- соответствующие значения 
.
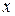4. 
Решить уравнение:
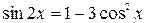
Решение. Заменяя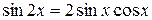 
и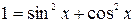 
, получим однородное уравнение:
,
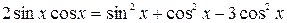или
.
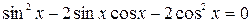Деля на (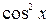 
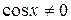), получим:
.
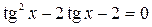Вводим новую переменную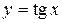 
и получаем квадратное уравнение относительно нее:
.
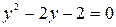Корни этого уравнения: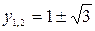 
. Далее получаем равносильную совокупность уравнений:
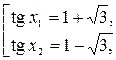
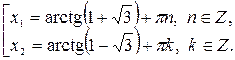
2. Уравнения, левая часть которых раскладывается на множители, а правая часть равна нулю.
Перенеся все члены любого уравнения в левую часть, его можно привести к виду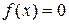 
.
Если левая часть этого уравнения раскладывается на сомножители, то каждый из них приравнивается к нулю, и уравнение распадается на несколько простых уравнений. Очень важно при этом иметь в виду, что корнями первоначального уравнения будут только те из корней полученных уравнений, которые входят в область определения первоначального уравнения.
