Твердое тело, движущееся в пространстве, как известно, обладает шестью степенями свободы – тремя поступательными и тремя вращательными. Для описания движения твердого тела выберем инерциальную систему отсчета 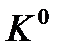 (с осями
(с осями 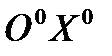 ,
, 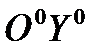 ,
, 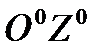 ), которую будем считать неподвижной. Эта система еще называется земной, поскольку может быть жестко связана с некоторым местом на поверхности земли. С телом свяжем жестко другую систему
), которую будем считать неподвижной. Эта система еще называется земной, поскольку может быть жестко связана с некоторым местом на поверхности земли. С телом свяжем жестко другую систему 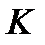 (с осями
(с осями 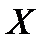 ,
,  ,
, 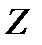 ), поместив ее начало в некоторую точку внутри тела, например, в геометрический центр
), поместив ее начало в некоторую точку внутри тела, например, в геометрический центр  (рис.2.1).
(рис.2.1).
 Рис.2.1 – Рассматриваемые системы координат
Рис.2.1 – Рассматриваемые системы координат
В качестве обобщенных координат, определяющих положение тела, удобно взять три координаты начала системы  -
- 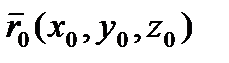 и три угла, характеризующих ориентацию осей
и три угла, характеризующих ориентацию осей 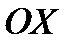 ,
, 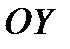 и
и 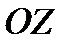 по отношению к осям
по отношению к осям 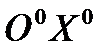 ,
, 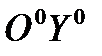 ,
, 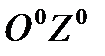 . Названные оси образуют друг с другом девять углов, однако независимыми оказываются только три из них. Обычно в качестве трех углов, определяющих взаимную ориентацию осей систем
. Названные оси образуют друг с другом девять углов, однако независимыми оказываются только три из них. Обычно в качестве трех углов, определяющих взаимную ориентацию осей систем 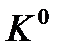 и
и 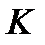 , используются эйлеровы углы
, используются эйлеровы углы 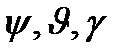 . Эти углы вводятся следующим образом [2,4,5].
. Эти углы вводятся следующим образом [2,4,5].
Для удобства будем рассматривать еще одну систему координат – 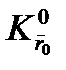 , которая является местной для тела, т.е. ее начало в каждый момент совпадает с центром
, которая является местной для тела, т.е. ее начало в каждый момент совпадает с центром  тела, а оси ориентированы по направлениям соответствующих осей земной неподвижной системы
тела, а оси ориентированы по направлениям соответствующих осей земной неподвижной системы 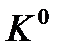 .
.
Пусть первоначально оси связанной с телом системы 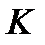 были параллельны соответствующим осям системы
были параллельны соответствующим осям системы 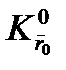 . Затем тело совершило некоторый поворот относительно
. Затем тело совершило некоторый поворот относительно 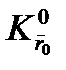 , в результате чего ориентация осей
, в результате чего ориентация осей 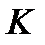 в пространстве изменилась.
в пространстве изменилась.
Любой такой поворот можно представить как сумму трех последовательных поворотов системы 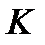 относительно системы
относительно системы 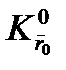 : первый поворот осуществляется вокруг оси
: первый поворот осуществляется вокруг оси 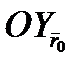 на угол
на угол 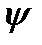 (рис.2.2). Второй поворот происходит вокруг оси
(рис.2.2). Второй поворот происходит вокруг оси 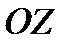 связанной системы координат на угол
связанной системы координат на угол 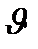 , и третий поворот - вокруг оси
, и третий поворот - вокруг оси 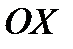 системы
системы 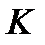 на угол
на угол  . Положительные направления поворотов соответствуют вращению против часовой стрелки, если смотреть с концов соответствующих осей вращения.
. Положительные направления поворотов соответствуют вращению против часовой стрелки, если смотреть с концов соответствующих осей вращения.
Из этих рисунков видно, что угол 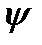 , называемый углом рысканья, есть угол между проекцией оси продольной симметрии тела
, называемый углом рысканья, есть угол между проекцией оси продольной симметрии тела 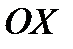 на горизонтальную плоскость
на горизонтальную плоскость 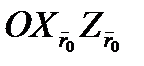 и направлением оси
и направлением оси 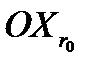 местной системы
местной системы 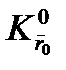 ;
; 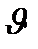 (угол тангажа) есть угол между продольной осью
(угол тангажа) есть угол между продольной осью 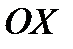 и горизонтальной плоскостью
и горизонтальной плоскостью 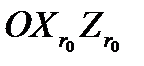 местной системы
местной системы 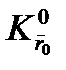 ;
;  (угол крена) - угол между осью
(угол крена) - угол между осью 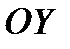 связанной системы и вертикальной плоскостью, проходящей через оси
связанной системы и вертикальной плоскостью, проходящей через оси 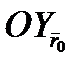 и
и 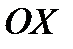 .
.
Связь между земной и связанной системами координат дается оператором вращения (с матрицей А), который преобразует компоненты произвольного вектора, заданного в земной системе координат 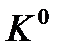 , в компоненты этого же вектора в связанной системе
, в компоненты этого же вектора в связанной системе 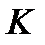 . Связь между компонентами матрицы
. Связь между компонентами матрицы 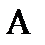 - направляющими косинусами углов между соответствующими осями, и углами Эйлера дается выражением [2,3]:
- направляющими косинусами углов между соответствующими осями, и углами Эйлера дается выражением [2,3]:
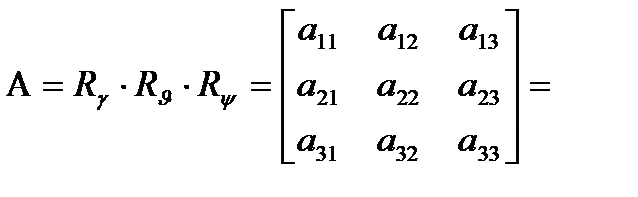
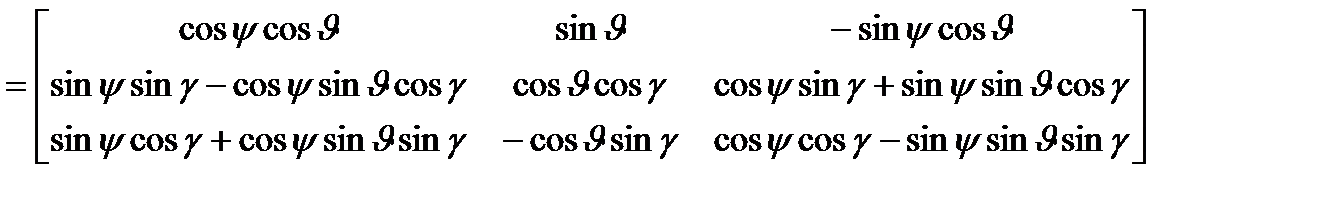 , (2.1)
, (2.1)
где операторы
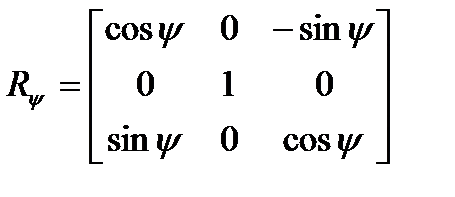 ,
, 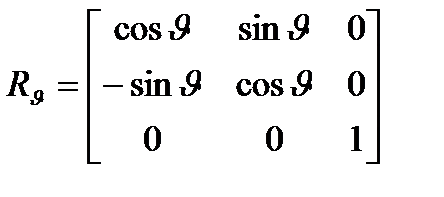 ,
, 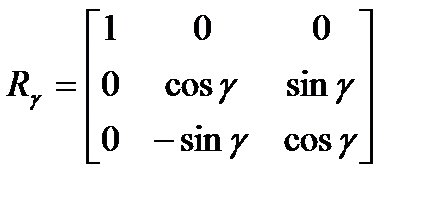
представляют собой операторы частичных (называемых также элементарными) поворотов осей связанной системы: 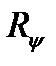 характеризует поворот относительно оси
характеризует поворот относительно оси 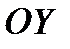 (или
(или 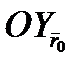 , в начальном положении эти оси совпадают) на угол
, в начальном положении эти оси совпадают) на угол 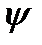 ,
,  - поворот относительно оси
- поворот относительно оси 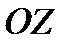 на угол
на угол 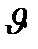 ,
, 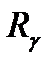 - поворот вокруг оси
- поворот вокруг оси 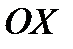 на угол
на угол 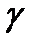 .
.
Скорости изменения углов выражаются через компоненты вектора угловой скорости 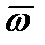 следующим образом:
следующим образом:
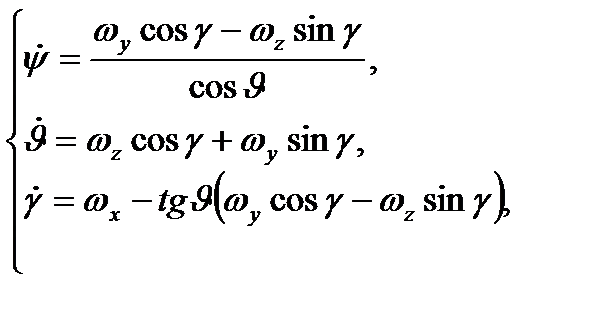 (2.3)
(2.3)
В систему уравнений кинематики твердого тела входят уравнения, связывающие компоненты скорости 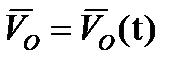 в связанной системе координат
в связанной системе координат 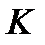 и компоненты той же скорости в земной базовой системе
и компоненты той же скорости в земной базовой системе 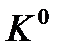 . Эти уравнения определяются линейным оператором
. Эти уравнения определяются линейным оператором 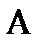 (для простоты используем обозначение
(для простоты используем обозначение 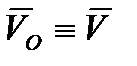 ):
):
Функция изменения скорости начала координат
 или
или 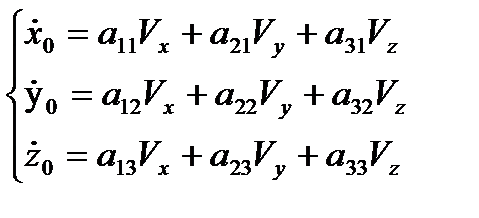 , (2.6)
, (2.6)
Уравнения (2.3) и (2.6) составляют систему уравнений кинематики твердого тела:
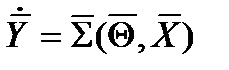 , (2.7)
, (2.7)
где 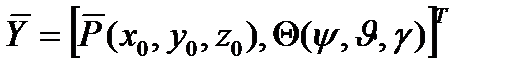 - вектор внешних координат, характеризующих положение и ориентацию связанной системы относительно базовой;
- вектор внешних координат, характеризующих положение и ориентацию связанной системы относительно базовой; 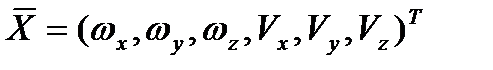 - вектор внутренних координат – проекций на связанные оси векторов линейной и угловой скоростей;
- вектор внутренних координат – проекций на связанные оси векторов линейной и угловой скоростей; 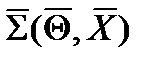 - вектор кинематических связей, состоящий из вектора линейных скоростей
- вектор кинематических связей, состоящий из вектора линейных скоростей 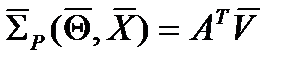 и вектора угловых скоростей
и вектора угловых скоростей 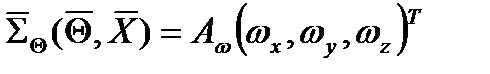 .
.
 2015-01-21
2015-01-21 827
827








