Уравнение Ньютона, соответствующее движению центра  связанной системы
связанной системы 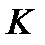 в случае, когда
в случае, когда  совпадает с центром инерции тела, имеет вид:
совпадает с центром инерции тела, имеет вид:
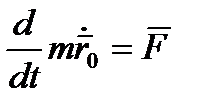 , (2.8)
, (2.8)
где 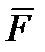 - результирующая сила, действующая на тело.
- результирующая сила, действующая на тело.
Заметим, что уравнение (2.8) записано в базовой системе координат. При решении задач, связанных с организацией автономного функционирования, самоуправления подвижного объекта необходимо все уравнения динамики писать в связанной системе, т.е. все входящие в эти уравнения величины должны представлять собой компоненты физических векторов по осям системы 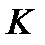 .
.
Поэтому получим уравнение, аналогичное (2.8), в связанной системе 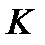 .
.
Хотя модуль вектора скорости движения центра масс, рассматривается он в системе 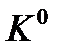 или в
или в 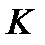 , одинаков, однако для наглядности будем обозначать этот вектор, когда он наблюдается в системе
, одинаков, однако для наглядности будем обозначать этот вектор, когда он наблюдается в системе 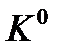 , как
, как 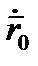 , а когда он наблюдается в системе
, а когда он наблюдается в системе 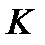 - через
- через 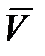 .
.
Тогда производные по времени вектора скорости центра масс тела, наблюдаемые в системах 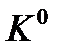 и
и 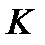 , связаны между собой следующим образом:
, связаны между собой следующим образом:
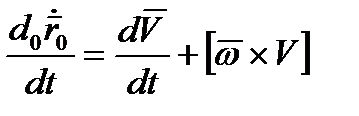 . (2.9)
. (2.9)
Согласно (2.9) первое векторное уравнение динамики твердого тела относительно связанной системы координат имеет вид:
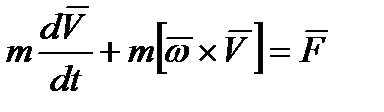 . (2.10)
. (2.10)
Заметим, что если перенести второе слагаемое в левой части (2.10) в правую часть, то его можно истолковать как дополнительную инерциальную силу.
Выражение (2.10) было выведено в предположении, что начало системы координат 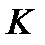 , жестко связанной с движущимся телом, совпадает с его центром инерции. Однако иногда приходится выбирать начало системы
, жестко связанной с движущимся телом, совпадает с его центром инерции. Однако иногда приходится выбирать начало системы 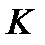 не совпадающим с центром инерции. Например, в случае с дирижаблем удобнее выбрать начало системы
не совпадающим с центром инерции. Например, в случае с дирижаблем удобнее выбрать начало системы 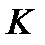 в геометрическом центре корпуса дирижабля, точнее, в центре масс такого эквивалентного данному дирижабля, который бы имел ту же форму, что и корпус данного дирижабля, и функцию массовой плотности, равномерно распределенную по всему его объему. При этом центр масс реального дирижабля может быть смещенным по отношению к такому геометрическому центру как вследствие неравномерности распределения плотности по объему корпуса, так и вследствие наличия стабилизаторов, карданового подвеса с двигателями и прочего оснащения, что приводит к смещению центра масс из геометрического центра.
в геометрическом центре корпуса дирижабля, точнее, в центре масс такого эквивалентного данному дирижабля, который бы имел ту же форму, что и корпус данного дирижабля, и функцию массовой плотности, равномерно распределенную по всему его объему. При этом центр масс реального дирижабля может быть смещенным по отношению к такому геометрическому центру как вследствие неравномерности распределения плотности по объему корпуса, так и вследствие наличия стабилизаторов, карданового подвеса с двигателями и прочего оснащения, что приводит к смещению центра масс из геометрического центра.
Пусть 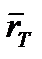 - радиус вектор, проведенный из
- радиус вектор, проведенный из  - начала системы
- начала системы 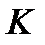 , до точки центра масс
, до точки центра масс 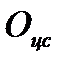 . Согласно формуле (2.5) для скорости начала координат
. Согласно формуле (2.5) для скорости начала координат  можем записать:
можем записать:
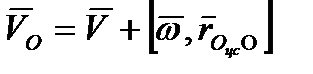 ,
,
где 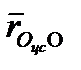 - радиус вектор, поведенный из точки центра масс
- радиус вектор, поведенный из точки центра масс 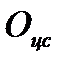 до начала координат системы
до начала координат системы 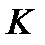 . Так как
. Так как 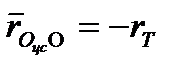 , то получим:
, то получим:
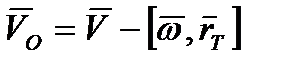 . (2.11)
. (2.11)
Подставляя (2.11) в (2.10), получим:
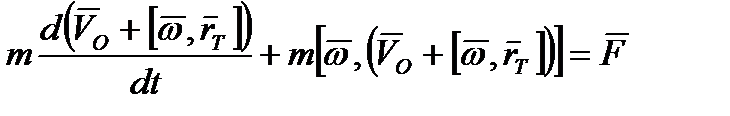 , (2.12)
, (2.12)
Это ур-ие можно преобразовать к ур-ия в проекциях.
 2015-01-21
2015-01-21 683
683








