Уравнение динамики вращательного движения, записанное в системе 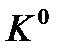 , имеет вид:
, имеет вид:
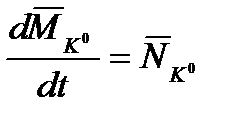 . (2.14)
. (2.14)
При рассмотрении моментов силы и импульса относительно местной подвижной системы 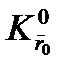 с центром в точке
с центром в точке  уравнение динамики примет вид [4-6]:
уравнение динамики примет вид [4-6]:
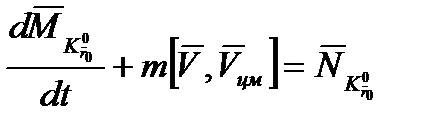 , (2.15)
, (2.15)
где
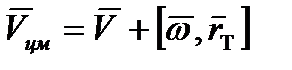 , (2.16)
, (2.16)
- скорость центра масс дирижабля. Уравнение (2.15) на основании (2.16) можно преобразовать к виду
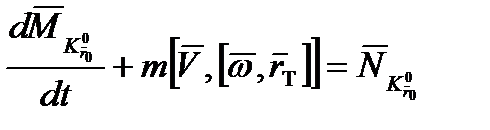 . (2.17)
. (2.17)
При рассмотрении вращательного движения тела в системе 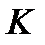 получим [6]:
получим [6]:
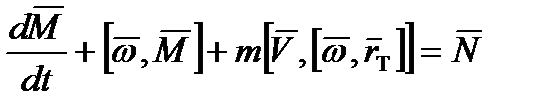 , (2.18)
, (2.18)
где 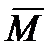 и
и 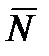 - наблюдаемые в системе
- наблюдаемые в системе 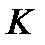 моменты импульса и силы, а также использовано равенство
моменты импульса и силы, а также использовано равенство 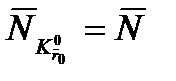 , которое говорит о том, что различие проекций вектора момента силы в системах
, которое говорит о том, что различие проекций вектора момента силы в системах 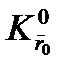 и
и 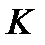 обусловлено только произвольностью ориентации соответствующих осей этих систем, а не угловой скоростью
обусловлено только произвольностью ориентации соответствующих осей этих систем, а не угловой скоростью 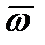 движения
движения 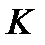 относительно
относительно 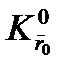 [4].
[4].
Момент импульса 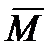 , наблюдаемый в неинерциальной системе
, наблюдаемый в неинерциальной системе 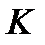 , представляется в виде [6]:
, представляется в виде [6]:
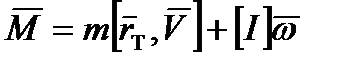 , (2.19)
, (2.19)
где 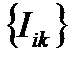 - тензор инерции тела.
- тензор инерции тела.
Уравнение динамики вращательного движения в общем случае:
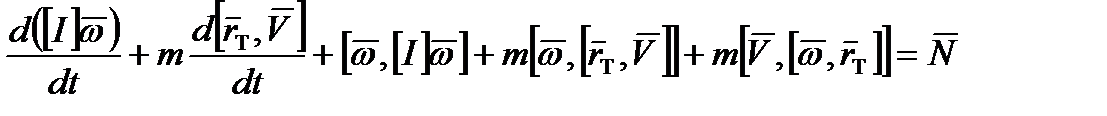 (2.21)
(2.21)
Уравнения (2.21) вместе с (2.12) образуют систему уравнений динамики твердого тела относительно связанной системы 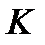 .
.
 2015-01-21
2015-01-21 563
563








