2015-01-21
1029
Систему равенств (2.3), (2.6), (2.13) и (2.22), описывающих кинематику и динамику дирижабля, и, в случае необходимости, векторное уравнение динамики приводов (2.47), можно представить в следующем матричном виде, удобном для анализа управляемости подвижного твердого тела [2]:
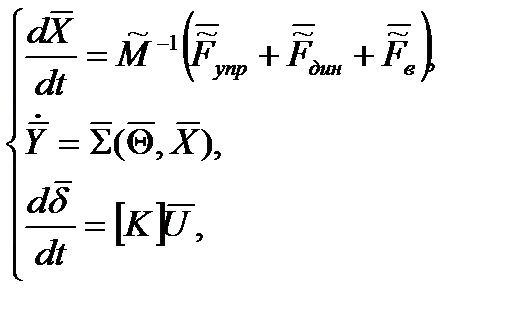(2.48)
где 
- обобщенный вектор управляющих воздействий,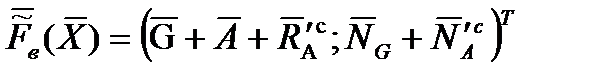 
- обобщенный вектор измеряемых и неизмеряемых внешних возмущений, 
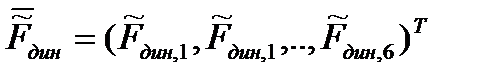- обобщенный вектор нелинейных элементов динамики, соответствующих нелинейным функциям от проекций линейной и угловой скоростей на связанные оси (эти нелинейные функции содержатся в левых частях равенств (2.13) и (2.22)), а также некоторым составляющим проекций аэродинамических силы и момента, зависящим от присоединенных масс тела (по этому поводу см. пункт 2.5.2.5, посвященный исследованию влияния инерционности сплошной среды); 
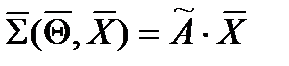, матрицы 
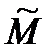и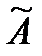 
имеют вид:
,
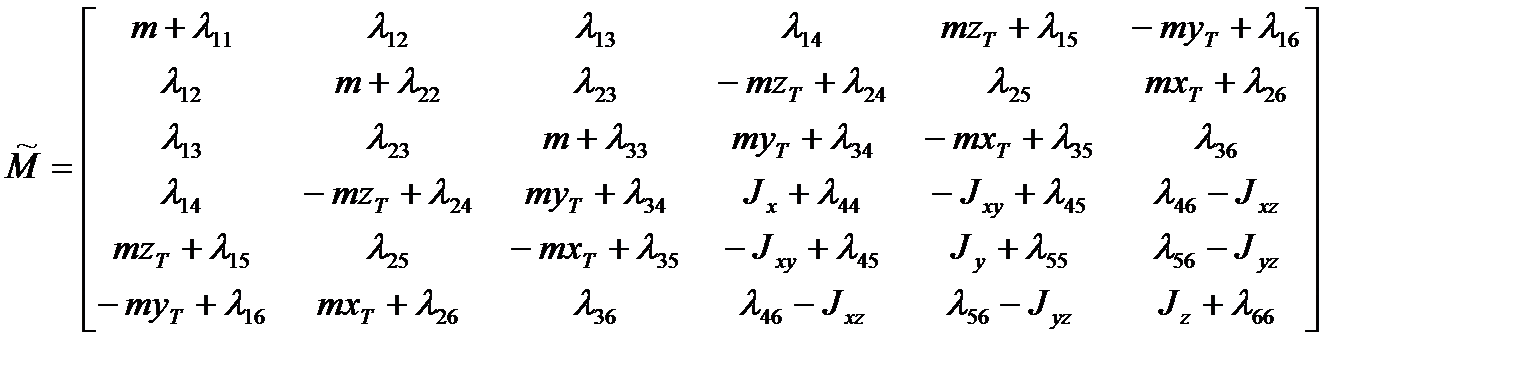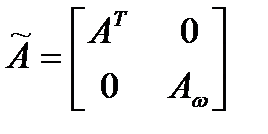, (2.49)
где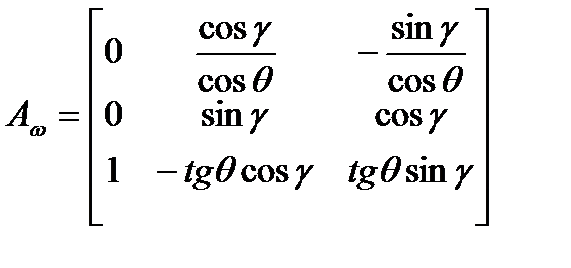 
, 
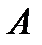- матрица вращения (2.1).
Из структуры матрицы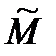 
видна роль присоединённых масс 
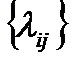, которые добавляются к соответствующим инерционным характеристикам твердого тела. Кроме того, элементы присоединенных масс входят также и в выражения для проекций вектора 
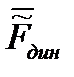нелинейных элементов динамики в (2.48).
|
|
|
Компоненты вектора 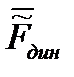при этом даются следующими выражениями:
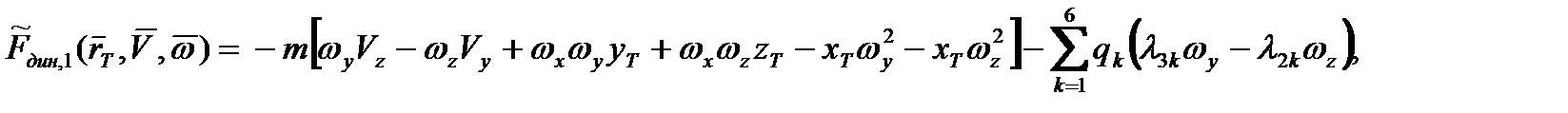
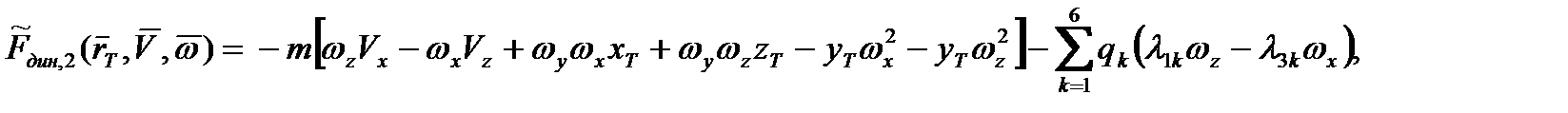
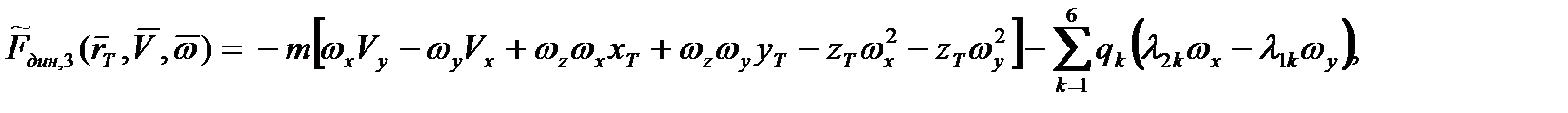
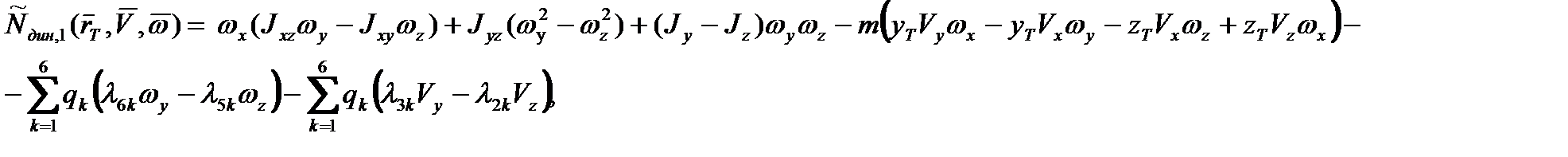
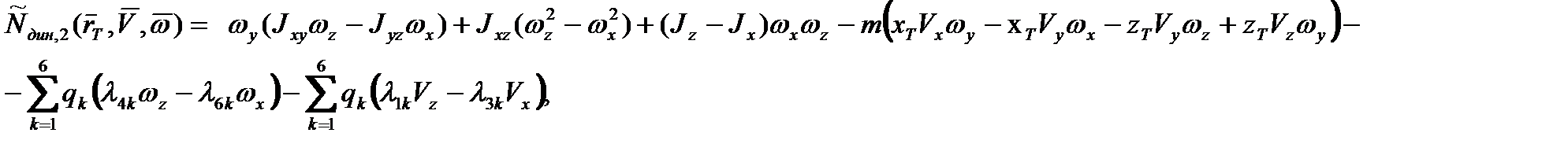
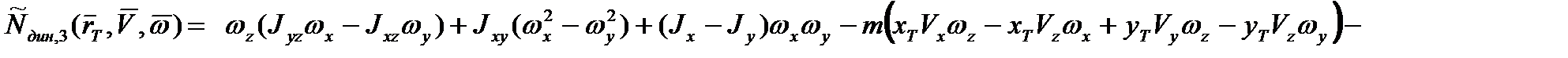
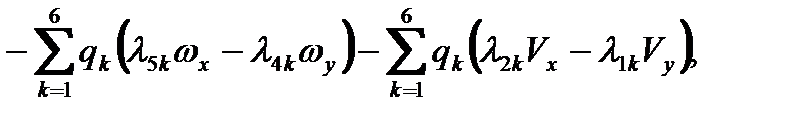. (2.50)
Внешние возмущающие воздействия представляются в следующем виде:
,
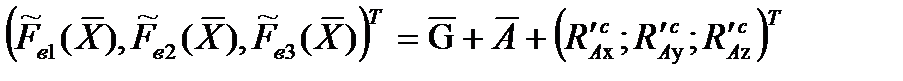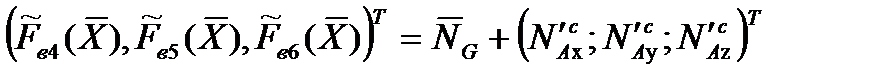, (2.51)
где проекции силы и момента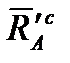 
, 
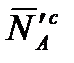представлены в виде, аналогичном (2.37), – через соответствующие им аэродинамические коэффициенты:
, 
, 
,
, 
, 
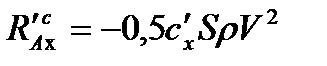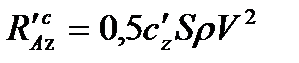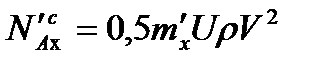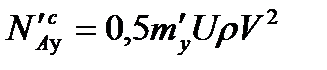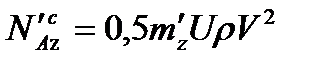. (2.52)
Нахождение векторов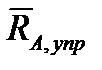 
и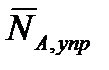 
, входящих наряду с силой и моментом двигателей 
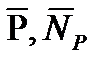в обобщенную управляющую силу 
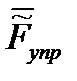, далее будет подробно рассмотрено.
Первое векторное уравнение в (2.47) содержит, таким образом, компоненты полных аэродинамических силы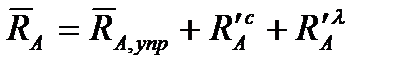 
и момента 
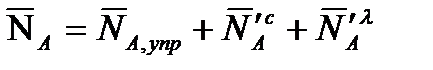, имеющих большое значение. Роль 
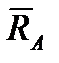и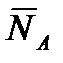 
растет с ростом скорости, однако даже при небольших скоростях при решении задач управления необходимо как можно более точно знать эти силы и моменты. Поэтому рассмотрим более подробно вопрос об определении этих величин.
Из выражений (2.31)-(2.36) видно, что проекции векторов аэродинамической силы и момента могут быть представлены в виде:
, 
,
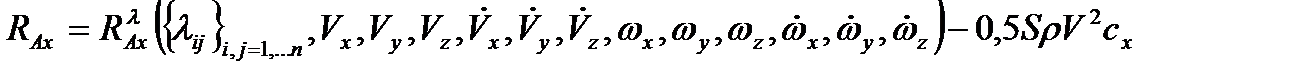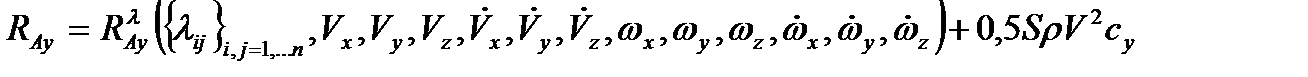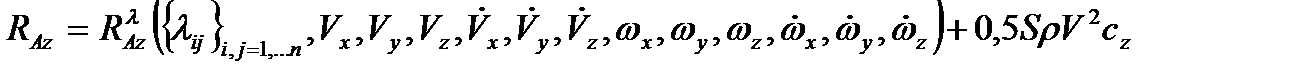, (2.53)
,
,
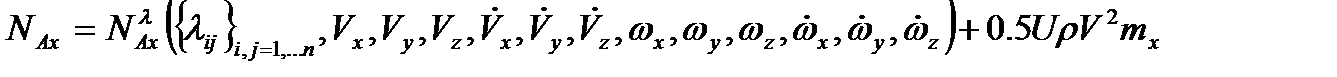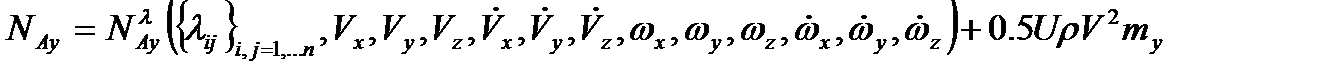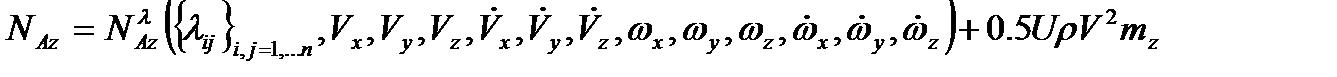, (2.54)
Первые слагаемые в (2.53),(2.54) описывают движение с ускорением, поэтому зависят от присоединенных масс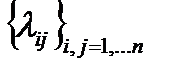 
, от проекций векторов поступательной и вращательной скоростей тела и их первых производных; 
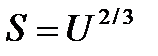- характерная площадь дирижабля, 
, 
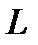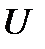- его длина и объем. Вторые слагаемые, в этих выражениях в каждый момент времени зависят от скорости движения 
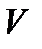, плотности воздуха 
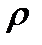и влияния формы тела на характер обтекания воздухом при данном режиме движения, т.е. от 
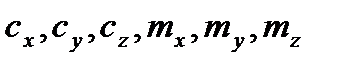- аэродинамических коэффициентов.
Если бы тело двигалось равномерно и прямолинейно, то первые слагаемые отсутствовали. В случае ускоренного движения дирижабля первые и вторые слагаемые сравнимы между собой, т.е. в общем случае ни одним нельзя пренебречь в сравнении с другим.
|
|
|
Смысл аэродинамических коэффициентов и присоединенных масс в общей динамике дирижабля мы в дальнейшем сможем выявить, рассмотрев кратко основные положения механики сплошных сред в следующем разделе 2.5.
В начале раздела 2.5 мы раскроем основные особенности аэродинамики дирижабля, которые выделяют его среди других летательных аппаратов. Эти особенности станут читателю более понятны после изучения следующих теоретических параграфов этого раздела.
