Движение тела в газе (так же как и в жидкости) невозможно описать, не пользуясь понятием распределенной силовой нагрузки – т.е. понятием распределения элементарных сил по поверхности тела, геометрическая сумма которых дает полную силу, воздействующую на тело со стороны сплошной среды.
Рисунок 7 – К определению распределенной силовой нагрузки, действующей на дирижабль
Для каждой точки 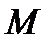 поверхности соприкосновения тела и сплошной среды выделим элементарную площадку
поверхности соприкосновения тела и сплошной среды выделим элементарную площадку 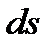 , принадлежащую этой поверхности и по величине гораздо меньше ее площади. Со стороны среды через эту площадку на тело будет действовать некоторая элементарная сила
, принадлежащую этой поверхности и по величине гораздо меньше ее площади. Со стороны среды через эту площадку на тело будет действовать некоторая элементарная сила 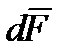 , равно как и на жидкость со стороны тела будет действовать противоположная по направлению сила такой же величины.
, равно как и на жидкость со стороны тела будет действовать противоположная по направлению сила такой же величины.
Разложим эту силу 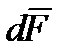 на две составляющие:
на две составляющие: 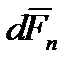 и
и 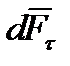 , т.е.
, т.е. 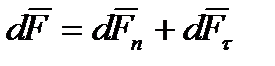 , где
, где 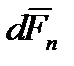 - составляющая силы
- составляющая силы 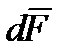 , нормальная к поверхности тела в данной точке
, нормальная к поверхности тела в данной точке 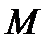 ,
, 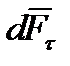 - составляющая силы
- составляющая силы 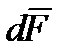 , касательная к поверхности тела в данной точке
, касательная к поверхности тела в данной точке 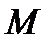 . Тогда плотность силы
. Тогда плотность силы 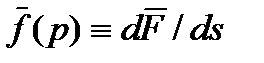 в данной точке
в данной точке 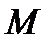 представим в виде
представим в виде 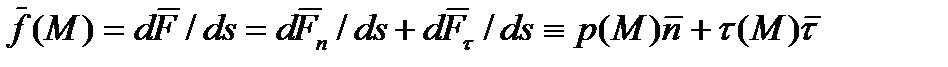 , где
, где 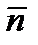 и
и 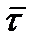 единичные орты по нормальному и касательному направлениям, соответствующим вектору
единичные орты по нормальному и касательному направлениям, соответствующим вектору 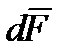 ;
; 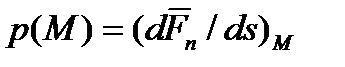 - давление, оказываемое жидкостью на тело в данной точке
- давление, оказываемое жидкостью на тело в данной точке 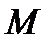 ,
, 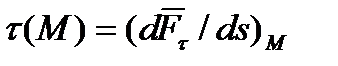 - касательное напряжение, возникающее в точке
- касательное напряжение, возникающее в точке 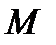 как результат взаимодействия трения между жидкостью и телом.
как результат взаимодействия трения между жидкостью и телом.
|
|
|
Заметим, что величины 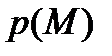 и
и 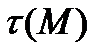 по смыслу эквивалентны нормальным и касательным напряжениям, действующим на частицу сплошной среды со стороны соседних с ней частиц этой среды.
по смыслу эквивалентны нормальным и касательным напряжениям, действующим на частицу сплошной среды со стороны соседних с ней частиц этой среды.
Указанную систему сил, распределенных по поверхности движущегося тела (рис.2.10), можно, однако, свести к равнодействующей силе 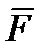 относительно некоторой точки, называемой центром давления тела (точка
относительно некоторой точки, называемой центром давления тела (точка  на рис.2.10). Положение центра давления в общем случае меняется с течением времени [9,10,13,14].
на рис.2.10). Положение центра давления в общем случае меняется с течением времени [9,10,13,14].
Для симметричных тел эта точка расположена на одной из основных осей – продольной оси летательного аппарата, проходящей через центр масс, или оси симметрии тела вращения.
Множество элементарных сил, распределенных по поверхности тела и действующих на неё, порождает множество элементарных моментов сил, сумма векторов которых есть эквивалентный равнодействующий момент 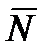 .
.
Воздействие сплошной средына тело сильно зависит от вязкости среды. Чем больше вязкость среды, тем больший по толщине приповерхностный слой сплошной среды становится возмущенным в результате движения в ней тела [10,11,13,14].
Свойство вязкости сплошной среды определяет касательные напряжения – напряжения трения.
Вид движения – турбулентный или ламинарный – определяется характерным параметром обтекания, показывающим степень влияния сил трения за счет вязкости на характер обтекания тела – числом Рейнольдса [12]:
|
|
|
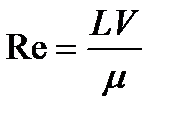 , (2.56)
, (2.56)
где 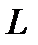 - линейный размер тела по направлению движения невозмущенного потока,
- линейный размер тела по направлению движения невозмущенного потока, 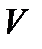 - скорость невозмущенного потока,
- скорость невозмущенного потока, 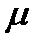 - динамический коэффициент вязкости.
- динамический коэффициент вязкости.
Согласно гипотезе, высказанной впервые Ньютоном, в ламинарном потоке трение возникает как результат диффузии молекул из одного слоя в другой, что приводит к изменению скорости течения, т.е. появлению относительного движения частиц газа в слоях. Согласно этой гипотезе, напряжение трения пропорционально для данных условий величине скорости этого относительного движения 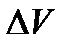 , приходящейся на единицу расстояния между слоями
, приходящейся на единицу расстояния между слоями 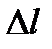 с относительно перемещающимися частицами. Если устремить расстояние между слоями к нулю
с относительно перемещающимися частицами. Если устремить расстояние между слоями к нулю 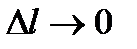 , то придем к случаю соприкосновения слоев, когда напряжение трения определяется градиентом скорости в данной точке [10]:
, то придем к случаю соприкосновения слоев, когда напряжение трения определяется градиентом скорости в данной точке [10]:
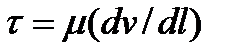 , (2.57)
, (2.57)
где 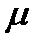 - динамический коэффициент вязкости, зависящий от свойств жидкости, а также в каждой точке пространства
- динамический коэффициент вязкости, зависящий от свойств жидкости, а также в каждой точке пространства 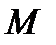 от температуры
от температуры 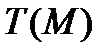 и давления
и давления 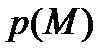 жидкости в этой точке.
жидкости в этой точке.
Градиент скорости имеет наибольшие значения вблизи стенки, так как вязкая среда испытывает торможение вследствие прилипания к поверхности обтекаемого тела. Скорость потока изменяется от нуля на стенке (рис.8) и постепенно увеличивается по мере удаления от поверхности. В соответствии с этим изменяется напряжение трения – у стенки оно значительно больше, чем вдали от нее. Тонкий слой жидкости, прилегающий к поверхности, характеризующийся большими градиентами скорости по нормали к поверхности и, следовательно, большими напряжениями трения, называется пограничным слоем.
Рисунок 2.8 – Профиль скорости в пограничном слое: а) - для ламинарного слоя, б) – для турбулентного слоя
Распределение скорости по сечению пограничного слоя зависит от характера течения. При турбулентном течении указанное распределение характеризуется большим градиентом скорости вблизи поверхности, чем в случае ламинарного течения (рис.2.8), вместе с тем среднее значение этого градиента (если усреднять по всему пограничному слою) больше при ламинарном потоке.
За пределами пограничного слоя расположена часть потока, где градиенты скорости и силы трения малы. Эту часть потока называют внешним свободным течением. При исследовании внешнего течения влиянием сил вязкости пренебрегают. Скорость в пограничном слое по мере удаления от стенки увеличивается, приближаясь асимптотически к теоретическому значению, соответствующему обтеканию невязкой жидкостью, т.е. к значению скорости во внешнем потоке на границе слоя. При еще большем удалении от поверхности тела поток становится практически невозмущенным. Он характеризуется невозмущенными давлением 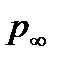 , плотностью
, плотностью 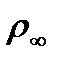 , температурой
, температурой 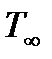 и скоростью относительного движения
и скоростью относительного движения 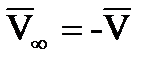 , где
, где 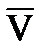 - скорость тела, движущегося в сплошной среде.
- скорость тела, движущегося в сплошной среде.
Для учета специфических особенностей конкретной задачи обтекания тела и получения однозначного решения соответствующей системы дифференциальных уравнений аэродинамики необходимо еще указать начальные и граничные условия для рассматриваемой задачи [9,10,13].
Начальные условия определяют состояние движения сплошной среды в начальный момент времени 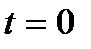 :
:
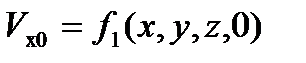 ,
, 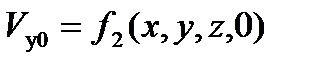 и т.д.
и т.д.
В случае установившегося движения надобность в задании начальных условий отпадает.
Граничные условия определяют особые условия движения сплошной среды на ее границах с твердыми телами, на свободной поверхности этой среды и на поверхностях раздела несмешивающихся сплошных сред. Рассмотрим некоторые типы граничных условий.
При пренебрежении сжимаемостью и вязкостью воздух ведет себя так, как несжимаемая идеальная жидкость, т.е. несжимаемая жидкость без трения. В этом случае в точках поверхности неподвижной твердой стенки нормальная к поверхности 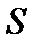 составляющая скорости газа равна нулю:
составляющая скорости газа равна нулю: 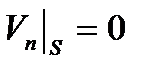 (условие скольжения);
(условие скольжения);
|
|
|
При учете вязкости сплошной среды в точках поверхности 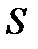 неподвижной стенки скорость этой среды равна нулю (условие прилипания):
неподвижной стенки скорость этой среды равна нулю (условие прилипания): 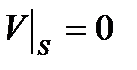 . В реальности имеет место именно этот случай: поверхность твердого тела как бы тормозит частицы жидкости.
. В реальности имеет место именно этот случай: поверхность твердого тела как бы тормозит частицы жидкости.
Однако граничное условие для идеальной жидкости 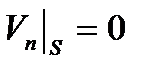 также широко используется в приближенных расчетах. Одна из причин этого заключается в том, что пограничный слой, внутри которого скорость жидкости замедляется существенно, весьма тонок в сравнении с размерами тела. Причем, как мы уже видели (рис.2.8) скорость частиц резко возрастает по мере удаления от поверхности тела, достигая значения на границе слоя, примерно равного
также широко используется в приближенных расчетах. Одна из причин этого заключается в том, что пограничный слой, внутри которого скорость жидкости замедляется существенно, весьма тонок в сравнении с размерами тела. Причем, как мы уже видели (рис.2.8) скорость частиц резко возрастает по мере удаления от поверхности тела, достигая значения на границе слоя, примерно равного 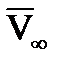 . За этим тонким слоем сплошная среда движется практически по законам свободного скольжения идеальной жидкости [9,10,13].
. За этим тонким слоем сплошная среда движется практически по законам свободного скольжения идеальной жидкости [9,10,13].
 2015-01-21
2015-01-21 2648
2648








