2015-01-21
1670
Как было показано, в построении индексов возникает много дискуссионных вопросов. Индексы считаются построенными правильно, если они удовлетворяют ряду тестов. Эти тесты были сформулированы американским статистиком И. Фишером (1867 - 1947). Основные тесты таковы:
1. Тест обратимости во времени. Индексы, исчисленные в «прямом» и «обратном» направлениях, должны быть взаимообратными числами. Например, если индекс показывает, что уровень цен в отчетном периоде по сравнению с базисным повысился в два раза, то он должен отражать, что в базисном периоде цены были вполовину ниже, чем в отчетном, т. е.
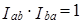, (10.20)
где а и b — сравниваемые периоды.
Очевидно, что наличие этого свойства желательно у любого индекса, ибо в таком случае сравнение между двумя состояниями не будет зависеть от того, какое из них принято за базу, особенно это важно при территориальных сравнениях.
2. Тест обратимости по факторам. Если поменять местами в индексе цен символы для цен и для количества, то мы должны получить индекс количества, который, будучи умножен на индекс цен, должен дать изменение общей стоимости товаров. Например, имеем:
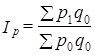
Если теперь поменять местами р и q, то получим:
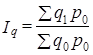
Произведение этих индексов
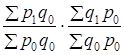
не равно индексу общей стоимости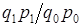 
. Следовательно, индексы этого типа не отвечают тесту обратимости факторов. Тесту обратимости отвечает средний геометрический индекс (10.14). По этой причине он был назван И. Фишером идеальным индексом.
3. Тест кружного испытания (циркулярность). Если построен некоторый индекс для года а при базисном годе b и для года b при базисном годе с, то из них можно получить индекс года а при базисном годе с. Тест кружного испытания требует, чтобы Ia/c, основанный на промежуточных сравнениях, совпал с тем, какой мы получили бы при непосредственном сравнении а с с, т. е.
Ia/b · Ib/c = Ia/c
Это требование принято называть, в статистике «цепным тестом».
В случае взвешенных индексов этот тест выполняется только для индексов с постоянными весами. Особенно трудно обеспечить выполнение этого теста при сравнении с отдаленной базой. Легко сравнивать каждый из ряда лет с предыдущим, но нелегко сравнивать удаленные годы: произведение цепных сравнений (между прилежащими годами) может отличаться от результатов непосредственного сравнения лет в начале и конце периода. Тут возникает много экономических проблем — и постоянство весов (проблема выбора неизменных цен при построении индексов объема производства), и выделение сравнимого круга элементов на протяжении всего периода (сравнимого круга товаров, видов продукции труда и т. д.) при анализе изменений цен, заработной платы и т. п.
В этот же тест Фишер вводил условие круговой сходимости, которое гласит: если условия начального и конечного моментов времени совпадают по уровням цен и объемов товаров, то произведение индексов цен и объемов товаров за все подпериоды должно быть равно единице.
4. Соизмеримость. Численные значения индексов не должны зависеть от выбора единиц измерения объема товаров и цен.
5. Пропорциональность. Согласно данному тесту, если темпы роста всех цен (или объемов товаров) равны одному и тому же числу, то этому же числу должен быть равен индекс цен (или индекс объема).
6. Включение - исключение. Если к набору товаров, по которым вычисляются индексы, и объему товаров, добавить еще один товар, темпы роста цены (или объема) которого совпадают с первоначальным индексом, то первоначальный индекс цен (или объема) не должен измениться.
Как видим, формулировка всех тестов основана на логике построения экономико-статистических показателей.
Тесты сыграли большую роль в развитии методологии экономических индексов.
