| Наименование | Формула расчета | Что показывает индекс | Что показывает значение индекса, уменьшенное на 100%, т.е. 1-100 | Что показывает разность числителя и знаменателя |
| Индекс физического объема продукции | 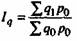 | Во сколько раз изменилась стоимость продукции в результате изменения ее объема, или сколько процентов составил рост (снижение) стоимости продукции из-за изменения ее физического объема | На сколько процентов изменилась стоимость продукции в результате изменения ее объема | На сколько рублей изменилась стоимость продукции в результате роста (уменьшения) ее объема |
| Индекс цен | 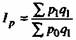 | Во сколько раз изменилась стоимость продукции в результате изменения цен, или сколько процентов составил рост (снижение) стоимости продукции из-за изменения цен | На сколько процентов изменилась стоимость продукции в результате изменения цен | На сколько рублей изменилась стоимость продукции в результате роста (уменьшения) цен |
| Индекс стоимости продукции (товарооборота) | 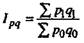 | Во сколько раз возросла (уменьшилась) стоимость продукции, или сколько процентов составил рост (снижение) стоимости продукции в текущем периоде по сравнению с базисным | На сколько процентов возросла (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным | На сколько рублей увеличилась (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным |
| Индекс физического объема | 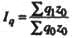 | Во сколько раз изменились издержки производства продукции в результате изменения объема ее производства, или сколько процентов составил рост (снижение) издержек производства продукции из-за изменения физического объема ее производства | На сколько процентов изменились издержки производства продукции в результате изменения объема ее производства | На сколько рублей изменились издержки производства продукции в результате роста (уменьшения) объема ее производства |
| Индекс себестоимости продукции | 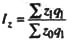 | Во сколько раз изменились издержки производства продукции в результате изменения себестоимости продукции, или сколько процентов составил рост (снижение) издержек производства продукции из-за изменения ее себестоимости | На сколько процентов изменились издержки производства продукции в результате изменения ее себестоимости | На сколько рублей изменились издержки производства в результате роста (уменьшения) себестоимости продукции |
| Индекс издержек производства | 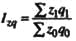 | Во сколько раз возросли (уменьшились) издержки производства продукции, или сколько процентов составил рост (снижение) издержек производства продукции в текущем периоде по сравнению с базисным | На сколько процентов возросли (уменьшились) издержки производства продукции в текущем периоде по сравнению с базисным | На сколько рублей увеличились (уменьшились) издержки производства продукции в текущем периоде по сравнению с базисным |
| Индекс физического объема продукции | 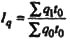 | Во сколько раз изменились затраты времени на производство продукции в результате изменения объема ее производства, или сколько процентов составил рост (снижение) затрат времени на производство продукции из-за изменения физического объема ее производства | На сколько процентов изменились затраты времени на производство продукции в результате изменения объема ее производства | На сколько человеко-часов возросли (уменьшились) затраты времени на производство продукции в результате роста (уменьшения) объема производства продукции |
| Индекс производительности труда по трудовым затратам | 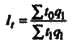 | Во сколько раз увеличилась (уменьшилась) производительность груда, или сколько процентов составило снижение (рост) производительности труда в текущем периоде по сравнению с базисным | На сколько процентов изменилась производительность труда в текущем периоде по сравнению с базисным | Абсолютный размер экономии (перерасхода) затрат живого труда в связи с ростом (уменьшением) его производительности |
| Индекс затрат времени на производство продукции | 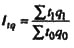 | Во сколько раз изменились затраты времени на производство продукции, или сколько процентов составил рост (снижение) затрат времени на производство продукции в текущем периоде по сравнению с базисным | На сколько процентов изменились затраты времени на производство продукции в текущем периоде по сравнению с базисным | На сколько человеко-часов увеличились (уменьшились) затраты на производство продукции в текущем периоде по сравнению с базисным |
Средний арифметический индекс физического объема продукции вычисляется по формуле:

Так как iq ∙ q0 = q1, то формула этого индекса легко преобразуется в формулу (12.14). Весами в формуле (12.19) является стоимость продукции базисного периода.
Средний арифметический индекс производительности труда определяется следующим образом:
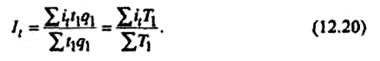
Так как it ∙ t1 = t0, то формула этого индекса может быть преобразована в агрегатный индекс трудоемкости продукции. Весами являются общие затраты времени на производство продукции в текущем периоде.
В статистике широко известен и другой средний арифметический индекс, который используется при анализе производительности труда. Он носит название индекса Струмилина и определяется следующим образом:
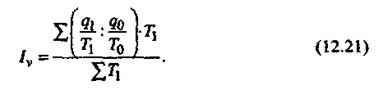
Индекс показывает, во сколько раз возросла (уменьшилась) производительность труда, или сколько процентов составил рост (снижение) производительности труда в среднем по всем единицам исследуемой совокупности.
Средние арифметические индексы чаще всего применяются на практике для расчета сводных индексов количественных показателей. При анализе качественных показателей данная форма индекса применяется для исчисления приведенных выше индексов (формулы (12.20) – (12.21)).
Индексы других качественных показателей (цен, себестоимости и т.д.) определяются по формуле средней гармонической взвешенной величины.
Средний гармонический индекс тождествен агрегатному, если индивидуальные индексы взвешены с помощью слагаемых числителя агрегатного индекса.
Например, индекс себестоимости можно исчислить так:
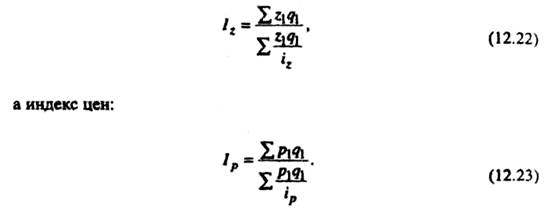
Таким образом, при определении среднего гармонического индекса себестоимости весами являются издержки производства текущего периода, а при вычислении индекса цен веса – стоимость продукции этого периода.
Рассчитаем средние индексы цен и физического объема продукции по данным табл. 12.1 (графы 11-12):
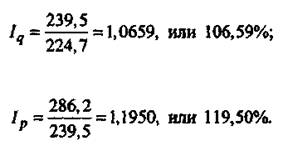
Этот же результат получился при расчете агрегатных индексов. Средние индексы широко используются для анализа рынка ценных бумаг. Наиболее известными являются индексы Доу-Джонса, Стэндарда и Пура.
Индекс Доу-Джонса (Dow Jones Industrial Average Index) определяется как средний арифметический индекс значений курсов акций, котирующихся на Нью-Йоркской фондовой бирже. Один сводный и три групповых индекса рассчитываются каждые полчаса, и ежедневно публикуется их значение на момент закрытия биржи. Групповые индексы определяются по ценам акций 30 промышленных, 20 транспортных и 15 компаний сферы услуг. Общий индекс рассчитывается по всем 65 компаниям. Их перечень был составлен в 1928 г. В качестве базисного выбран 1920 г. Первоначальная методика исчисления индекса была разработана основателем и редактором крупнейшей в США газеты «Уолл-стрит джорнел» Чарлзом Доу.
Индекс Стэндарда и Пура (Standard and Poor's 500 Stock Index) -индекс, рассчитываемый по курсам акций 500 крупнейших компаний Нью-Йоркской фондовой биржи как средний взвешенный показатель, учитывающий общее число выпущенных компанией акций. В число компаний, акции которых включены в индекс, входят 400 промышленных корпораций, 40 – финансовых, 20 – транспортных и 40 – сферы услуг.
31.Агрегатные и индивидуальные индексы их сущность и расчет.
Индекс — это обобщающий относительный показатель, характеризующий изменение уровня общественного явления во времени, по сравнению с программой развития, планом, прогнозом или его соотношение в пространстве.
Наиболее распространена сравнительная характеристика во времени. В этом случае индексы выступают как относительные величины динамики.
Индексный метод является также важнейшим аналитическим средством выявления связей между явлениями. При этом применяются уже не отдельные индексы, а их системы.
В статистической практике индексы применяются при анализе развития всех отраслей экономики, на всех этапах экономической работы. В условиях рыночной экономики особенно возросла роль индексов цен, доходов населения, фондового рынка и территориальных индексов.
Статистика осуществляет классификацию индексов по следующим признакам:
1. В зависимости от объекта исследования:
§ индексы объемных (количественных) показателей (индексы физического объема: товарооборота, продукции, потребления)
§ индексы качественных показателей (индексы цен, себестоимости, заработной плата)
К индексам объемных показателей относятся индексы физического объема: товарооборота, продукции, потребления материальных благ и услуг; а также других показателей, имеющих количественный характер: численности работников, посевных площадей и т.п. К индексам качественных показателей относятся индексы: цен, себестоимости продукции, заработной платы, производительности труда, урожайности и т.п.;
2. По степени охвата элементов совокупности:
§ индивидуальные индексы (дают сравнительную характеристику отдельных элементов явления)
§ общие индексы (характеризуют изменение совокупности элементов или всего явления в целом)
3. В зависимости от методологии исчисления общие индексы подразделяются на:
§ агрегатные (агрегатные индексы являются основной формой индексов и строятся как агрегаты путем взвешивания индексируемого показателя с помощью неизменной величины другого, взаимосвязанного с ним показателя).
§ средние (являются производными от агрегатных)
4. В зависимости от базы сравнения различают:
§ базисные (если при исчислении индексов за несколько периодов времени база сравнения остается постоянной)
§ цепные (если база сравнения постоянно меняется)
 2015-01-30
2015-01-30 3452
3452
