Основы теории. При проведении расчетов процессов и аппаратов химической технологии часто приходится определять количество подведенной или отведенной теплоты

При проведении расчетов процессов и аппаратов химической технологии часто приходится определять количество подведенной или отведенной теплоты. Наиболее просто это сделать, используя теплоемкость теплоносителей.

Удельной теплоемкостью называется количество теплоты, которое необходимо подвести к единице количества вещества, чтобы изменить его температуру на 1 градус. В связи с этим определением различают:

- удельную массовую теплоемкость

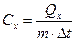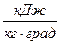, , откуда 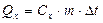, кДж; (1)

- удельную объемную теплоемкость

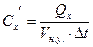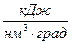, , откуда 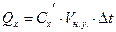, кДж; (2)

- удельную мольную теплоемкость

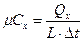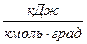, , откуда 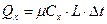, кДж, (3)

где m – масса газа, кг;

V_{н.у .}, нм³ – объем газа, приведенный к нормальным условиям (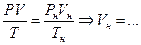, Р_н =760 мм рт. ст.=1,013×10⁵ Па, Т_н =273 К);

L – число киломолей вещества (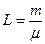), кмоль;

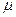- молекулярная масса газа, кг/кмоль;

_х – индекс, указывающий характер процесса подвода теплоты Q_x, например, при 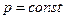(Q_p), при 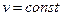(Q_v).

Поэтому различают:

С_р – изобарная теплоемкость,

С_v – изохорная теплоемкость.

Эти теплоемкости для идеальных газов связаны уравнением Майера:

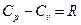. (4)

	С
		С=f(t)-нелинейная СХ=a+bt+et2+… а

t

Рис.1. Зависимость теплоемкости от температуры

б С=f(t)-линейная СХ=a+bt

СХ=const в

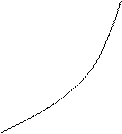
Теплоемкость зависит от температуры в общем случае нелинейно (рис. 1 а). При определении количества теплоты для нагревания при 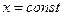от t₁ до t₂ обычно применяют средние теплоемкости 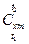(здесь индекс «m» означает «средний»!), которые при нелинейной зависимости рассчитываются по средним табличным значениям теплоемкостей 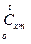в интервале температур от 0 до t:

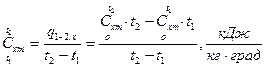, (5)

где 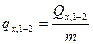- удельная массовая теплота, кДж/кг.

Следовательно

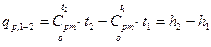, (6)

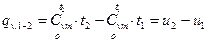, (7)

т.е. наиболее точно теплоту можно подсчитать как по значениям теплоемкостей, так и по значениям энтальпий h (при 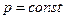) и внутренних энергий u (при 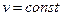). Значения 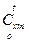, u и h приводятся в справочной литературе в виде таблиц /2/.

В пределе при уменьшении интервала температур в выражении (5) получим теплоемкость при заданной температуре t, называемую истинной теплоемкостью, С_х,ист.

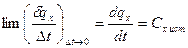. (8)

Со средней теплоемкостью она связана соотношением

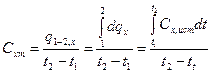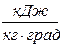, . (9)

Для приближенных расчетов можно учесть линейную зависимость теплоемкости от температуры (рис. 1б):

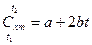, (10)

где a и b – индивидуальные коэффициенты (из таблиц /2/), .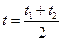

В соответствии с молекулярно-кинетической теорией внутренняя энергия газов распределяется равномерно по степеням свободы i поступательного и вращательного движения молекул. Для одноатомной молекулы i = 3 степеням свободы поступательного движения, т.е. изменяется положение молекулы в координатах x, y и z. Для двухатомных молекул к трем степеням свободы поступательного движения добавляются две степени свободы вращательного движения i = 3+2 = 5. С некоторой корректировкой для трех- и многоатомных газов число степеней свободы принимается равным i = 7.

Для идеальных газов при не очень высоких температурах на каждую степень свободы при 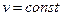расходуется энергия 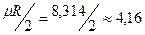кДж/(кмоль×град). Поэтому постоянные (рис.1, в) мольные теплоемкости 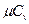можно определить по числам степеней свободы i, а 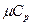- по (i + 2) из таблицы 1.

Таблица 1

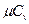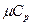Атомность газов	, кДж/(кмоль×град)	, кДж/(кмоль×град)
1 атомные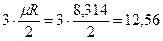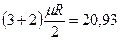
2 атомные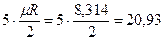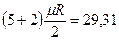
3 и многоатомные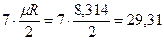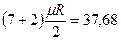

Для пересчета различных удельных теплоемкостей удобны соотношения:

, ; , ;

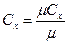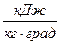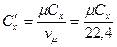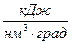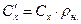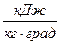, , (11)

где 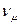- удельный объем 1 кмоля газа при нормальных условиях, .

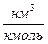Измерение теплоемкости С_рт воздуха
методом проточного калориметрирования

В лабораторном калориметре (рис. 2) к потоку газа подводится теплота от электронагревателя и измеряются все величины, необходимые для расчета теплоемкости: расход газа, количество подведенной теплоты, температуры газа на входе в калориметр и на выходе из него.

Расчетное уравнение для определения теплоемкости С_рт в таком калориметре может быть получено следующим образом. Запишем уравнение первого закона термодинамики для стационарного потока газа для сечения 1 на входе и 2 на выходе:

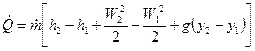, (12)

где 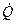- тепловой поток – количество теплоты, подведенной от электронагревателя в единицу времени, Дж/с или Вт;

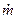- массовый расход газа, кг/с;

h – энтальпия газа, Дж/кг;

W – скорость газа, м/с;

g – ускорение свободного падения, м/с²;

y – координата сечений 1 и 2 канала по высоте, м.

В данном случае работой, затрачиваемой на изменение кинетической энергии газа 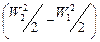, можно пренебречь, так как скорости газа W₁ и W₂ мало отличаются друг от друга. Работа, затрачиваемая на изменение потенциальной энергии 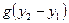, равна нулю, поскольку калориметр расположен горизонтально .

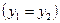Таким образом, уравнение (12) принимает вид:

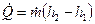. (13)

Проинтегрировав известное выражение для идеального газа

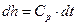(14)

в интервале температур от t₁ до t₂, получим:

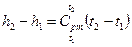, (15)

где 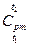- средняя теплоемкость при 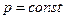в интервале температур от t₁ до t₂.

Из уравнений (13) и (15) следует:

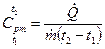. (16)