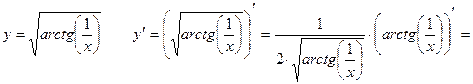
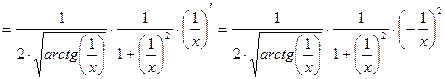
Задание 2. Вычислить производные функций.
1) 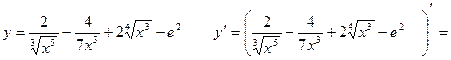
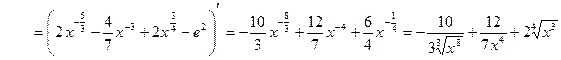
2) 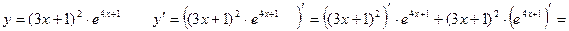
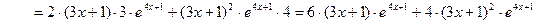
3) 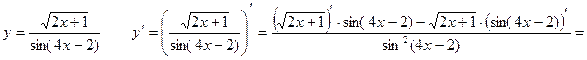
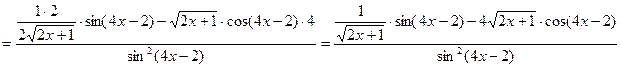
4) 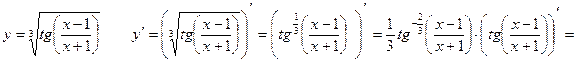
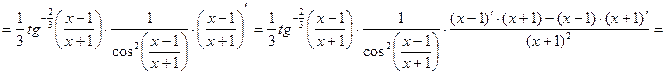
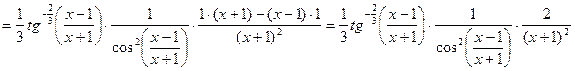
- Интервалы монотонности, экстремум функции одной переменной. Выпуклость, вогнутость функции, точки перегиба.
При построении графика функции 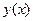 надо найти:
надо найти:
1) область определения 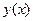
2) четность, нечетность 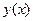
3) интервалы возрастания и убывания, экстремумы 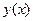
4) интервалы выпуклости и вогнутости, точки перегиба 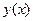
5) асимптоты 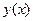
Экстремумы функции находятся по следующей схеме:
1) Находим производную, приравниваем к нулю, решаем это уравнение. Корни уравнения называются критическими точками. Корни знаменателя производной тоже называются критическими точками.
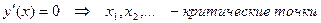
2) Критические точки отмечаем на прямой и на каждом интервале ставим знак
производной
3) Если 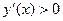 , на этом интервале функция возрастает, если
, на этом интервале функция возрастает, если 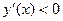 , на этом интервале функция убывает.
, на этом интервале функция убывает.
4) Если при переходе через критическую точку 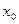 производная меняет свой знак с «плюс» на «минус», то в точке
производная меняет свой знак с «плюс» на «минус», то в точке 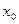 - максимум. Если при переходе через критическую точку
- максимум. Если при переходе через критическую точку 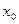 производная меняет свой знак с «минус» на «плюс», то в точке
производная меняет свой знак с «минус» на «плюс», то в точке 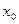 - минимум.
- минимум.
Пример. Найти экстремумы функции 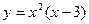
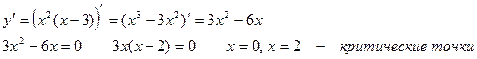
Отмечаем точки на оси и ставим знаки производной.

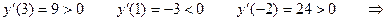
В точке 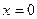 - максимум, в точке
- максимум, в точке 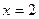 - минимум. Подставляя
- минимум. Подставляя 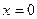 и
и 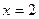 в функцию, найдем
в функцию, найдем 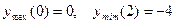 .
.
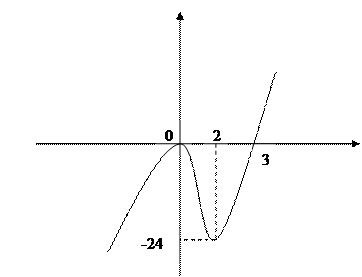
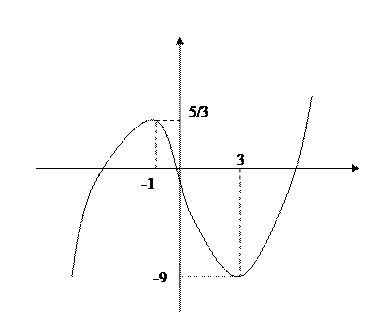
Пример. Построить график функции 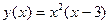
Найдем точки пересечения графика с осью 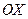 .
.
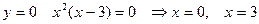
Экстремумы найдены в предыдущем примере.
. 
Пример. Построить график функции 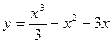
Найдем экстремумы.
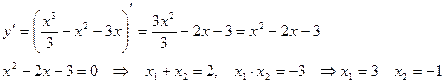
Отмечаем точки на прямой и на полученных интервалах ставим знаки производной.
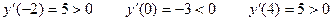
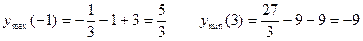

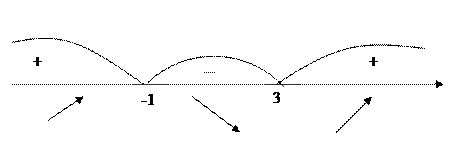
Строим график функции.
- Неопределенный интеграл.
Функция 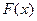 называется первообразной функции
называется первообразной функции 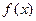 , если
, если 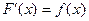 . Например, для
. Например, для 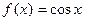 первообразной будет функция
первообразной будет функция 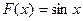 , так как
, так как 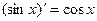 . Для функции
. Для функции 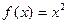 первообразной будет функция
первообразной будет функция 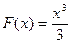 , так как
, так как 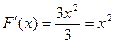 . Заметим, что если
. Заметим, что если 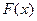 первообразная функции
первообразная функции 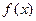 , то
, то 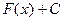 , где С – любое число, тоже первообразная функции
, где С – любое число, тоже первообразная функции 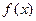 , так как
, так как 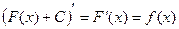 .
.
Множество первообразных функции 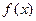 называется неопределенным интегралом от функции
называется неопределенным интегралом от функции 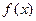 и обозначается
и обозначается 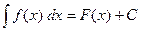 .
.
Например, 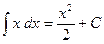 , так как
, так как 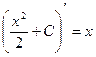
Запишем таблицу неопределенных интегралов.
1) 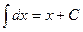 8)
8) 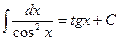
2) 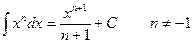 9)
9) 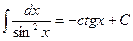
3) 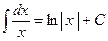 10)
10) 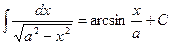
4) 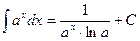 11)
11) 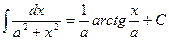
5) 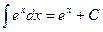 12)
12) 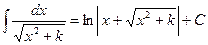
6) 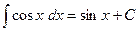 13)
13) 
7) 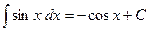
При нахождении неопределенного интеграла используют правила:
1. 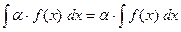 , то есть постоянный множитель выносится
, то есть постоянный множитель выносится
за знак интеграла
2. 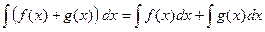 , то есть интеграл от суммы равен
, то есть интеграл от суммы равен
сумме интегралов.
Пример. 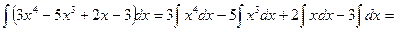
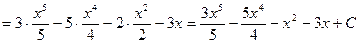
По определению 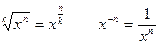 Например,
Например, 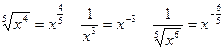
Пример. 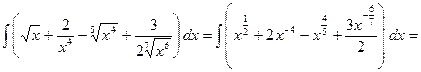
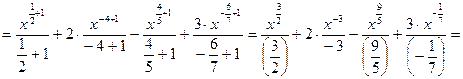
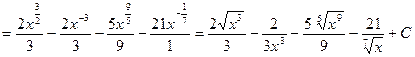
Пример. 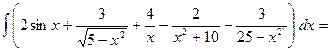
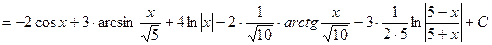
Дифференциалом функции 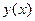 называется
называется 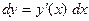
Например:
1) 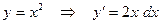
2) 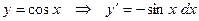
3) 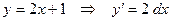
Пример. 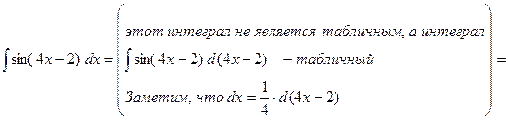
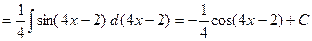
Пример. 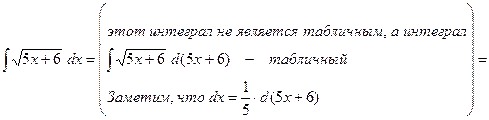
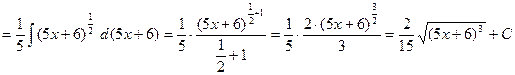
Пример. 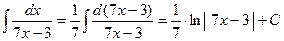
Пример. 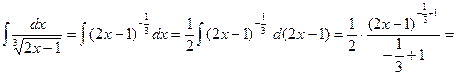
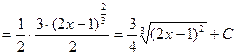
Выражение 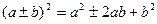 называется полным квадратом.
называется полным квадратом.
Пример. 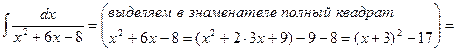
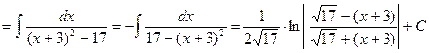
При нахождении интегралов иногда используют формулу 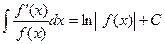
Например:
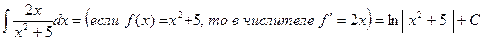
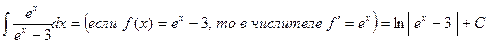
Пример. 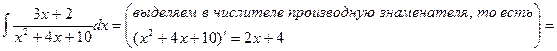
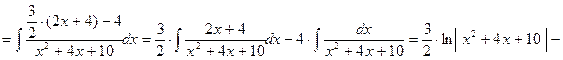
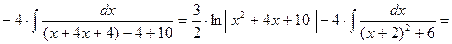
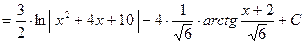
 2015-02-04
2015-02-04 466
466








