Пусть задана функция 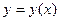 . Если при неограниченном приближении
. Если при неограниченном приближении 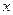 к
к 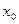 соответствующие значения функции неограниченно близко приближаются к числу А, то говорят, что функция
соответствующие значения функции неограниченно близко приближаются к числу А, то говорят, что функция 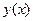 имеет предел и пишут
имеет предел и пишут 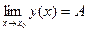 . При вычислении предела надо в функцию подставить
. При вычислении предела надо в функцию подставить 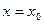 .
.
Пример. Вычислить предел функции.
1) 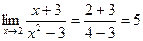 2)
2) 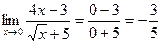
Функция 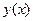 называется бесконечно большой (б.б.), если
называется бесконечно большой (б.б.), если 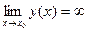 .
.
Функция 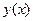 называется бесконечно малой (б.м.), если
называется бесконечно малой (б.м.), если 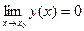 .
.
Пусть 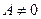 , тогда
, тогда 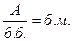 и
и 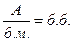 Эти правила для краткости можно записать следующим образом:
Эти правила для краткости можно записать следующим образом: 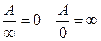
Пример. Вычислить предел функции.
1) 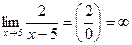 2)
2) 
При вычислении пределов после подстановки 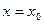 может получиться:
может получиться:
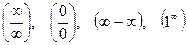 . Эти выражения называются неопределенностью. Для каждого вида неопределенности существует свой способ «раскрытия».
. Эти выражения называются неопределенностью. Для каждого вида неопределенности существует свой способ «раскрытия».
Для раскрытия этой неопределенности достаточно сравнить степени числителя и знаменателя по простому правилу:
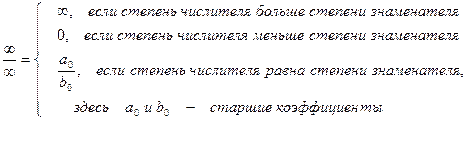
Пример. Вычислить предел функции.
1) 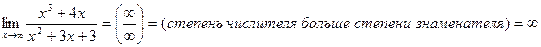
2) 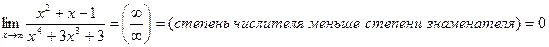
3) 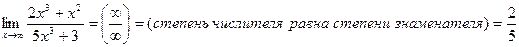
4) 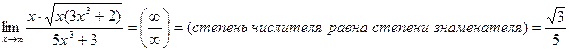
Для раскрытия этой неопределенности надо сократить дробь.
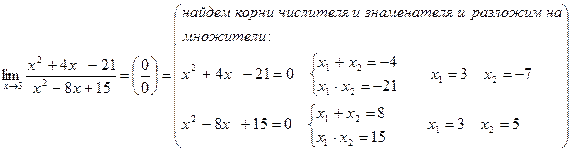
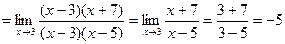
В некоторых случаях надо использовать таблицу эквивалентностей.
Две бесконечно малые величины 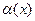 и
и 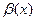 называются эквивалентными, если
называются эквивалентными, если 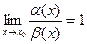 . Обозначение
. Обозначение 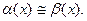 Приведем основные эквивалентности.
Приведем основные эквивалентности.
При 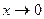 верно:
верно:
1) 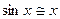
2) 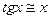
3) 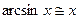
4) 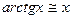
5) 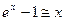
6) 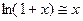
7) 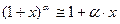
Пример. Вычислить предел функции.
1) 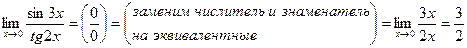
2) 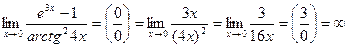
3) 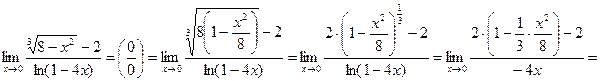
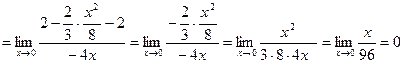
Неопределенность вида 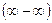 .
.
Для раскрытия этой неопределенности надо преобразовать выражение так, чтобы получилась неопределенность вида 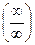 . Например, привести к общему знаменателю.
. Например, привести к общему знаменателю.
Пример. Вычислить предел функции.
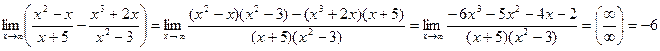
Неопределенность вида 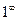 .
.
Для раскрытия этой неопределенности применяется второй замечательный предел:
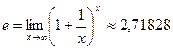
Пример. Вычислить предел функции.
1) 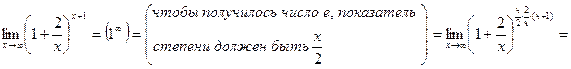
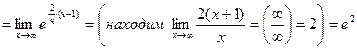
2) 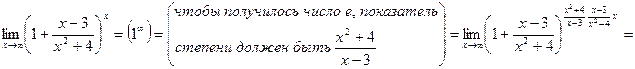
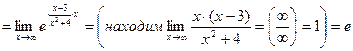
3) 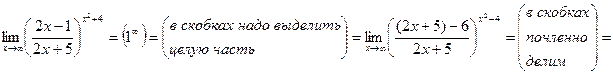
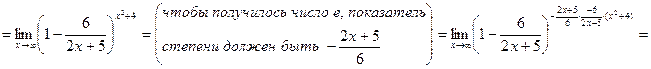
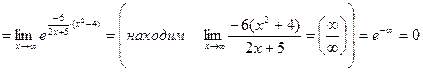
Задание 1. Вычислить пределы функций.
1) 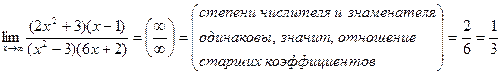
2) 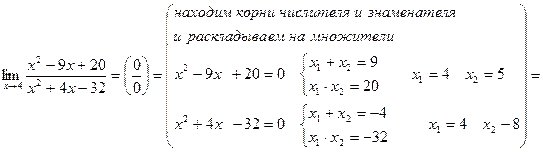
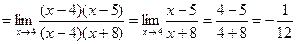
3) 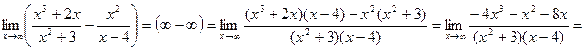
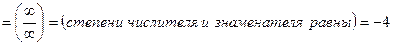
Задание 2. Вычислить предел функции.

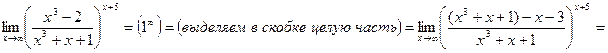
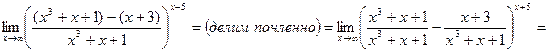
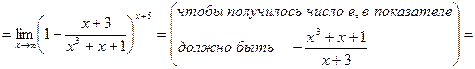
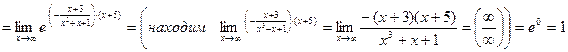
Задание 3. Вычислить пределы, используя эквивалентные бесконечно малые.
1) 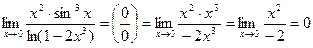
2) 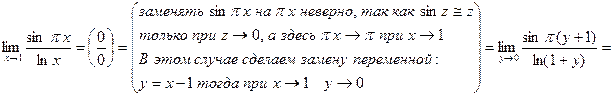

 2015-02-04
2015-02-04 3598
3598

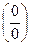 .
.