КРАТКАЯ ТЕОРИЯ: Крутильными колебаниями механической системы называются такие колебания, при которых отдельные элементы системы испытывают деформации кручения.
Примером крутильного маятника может служить массивный цилиндр А, подвешенный на стальной упругой проволоке (рис.1).
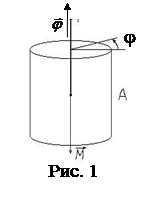 | Если вывести цилиндр из положения равновесия, повернув его на некоторый угол 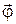 относительно оси О, и отпустить, то на него со стороны закрученной проволоки будет действовать вращающий момент относительно оси О, и отпустить, то на него со стороны закрученной проволоки будет действовать вращающий момент 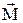 , стремящийся вернуть цилиндр в положение равновесия. Величина возвращающего момента, действующего со стороны стальной закрученной проволоки, в довольно больших пределах изменения угла пропорциональна этому углу: , стремящийся вернуть цилиндр в положение равновесия. Величина возвращающего момента, действующего со стороны стальной закрученной проволоки, в довольно больших пределах изменения угла пропорциональна этому углу: 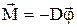 , (1) , (1) |
где D - коэффициент пропорциональности, называемый модулем кручения проволоки, зависит от материала и ее геометрических размеров. Знак "-" показывает, что векторы углового смещения 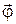 возвращающего момента
возвращающего момента 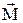 направлены в противоположенные стороны (рис.1).Основное уравнение динамики вращательного движения запишется в виде:
направлены в противоположенные стороны (рис.1).Основное уравнение динамики вращательного движения запишется в виде:
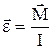 , (2)
, (2)
где I - момент инерции маятника, 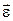 - его угловое ускорение,
- его угловое ускорение, 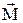 - возвращающий момент. В проекции на ось О:
- возвращающий момент. В проекции на ось О:
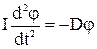 , или
, или 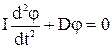 (3)
(3)
где 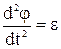 и
и 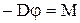 .
.
Решением дифференциального уравнения (3) является уравнение гармонических колебаний:
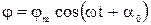 , (4)
, (4)
т.е. цилиндр будет совершать гармонические крутильные колебания с круговой частотой 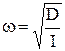 и периодом колебаний
и периодом колебаний
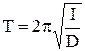 . (5)
. (5)
Таким образом, период крутильных колебаний цилиндра, подвешенного на стальной проволоке, определяется моментом инерции цилиндра и модулем кручения проволоки.
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА И МЕТОДИКА ИЗМЕРЕНИЙ.
Крутильный маятник, используемый в данной лабораторной работе, представляет собой горизонтальную платформу П (рис.2), подвешенную с помощью двух стальных проволок О1 и О2кнеподвижному кронштейну К.
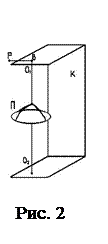 | Верхний конец проволоки О1 закреплен во втулке В с рукояткой Р. Если повернуть втулку В на некоторый угол относительно О1О2 и затем вернуть в прежнее положение, маятник будет совершать крутильные колебания с периодом Тn, значение которого согласно формуле (5) определяется моментом инерции платформы In и модулем кручения проволоки D: 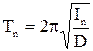 . (6) Если поместить на платформу какое-либо тело, то момент инерции системы будет равен сумме моментов инерции платформы и тела: . (6) Если поместить на платформу какое-либо тело, то момент инерции системы будет равен сумме моментов инерции платформы и тела: 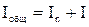 , (7) , (7) |
где I -момент инерции тела относительно оси, проходящей через центр платформы.
Период колебаний нагруженной платформы:
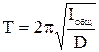 (8)
(8)
Из выражений (6) и (8) следует, что:
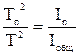 , (9)
, (9)
Таким образом, из (7) и (9) получаем:
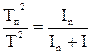 . (10)
. (10)
Выражение (10) позволяет вычислить моментинерции тела, расположенного на платформе, если известен момент инерции платформы:
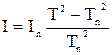 , (11)
, (11)
а также может быть использовано для нахождения момента инерции платформы, если известен момент инерции тела, лежащего на платформе:
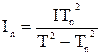 . (12)
. (12)
 2015-02-24
2015-02-24 1138
1138
