Центробежная сила инерции

Введение в рассмотрение сил инерции не является принципиально необходимым. В принципе любое движение можно всегда рассмотреть по отношению к инерциальной системе отсчета. Однако практически часто представляет интерес как раз движение тел по отношению к неинерциальным системам отсчета, например по отношению к земной поверхности. Использование сил инерции дает возможность решить соответствующую задачу непосредственно по отношению к такой системе отсчета, что часто оказывается значительно проще, чем рассмотрение движения в инерциальной системе.

Рассмотрим диск, вращающийся вокруг перпендикулярной к нему оси z ' с угловой скоростью ω (рис. 16). Вместе с диском вращается надетый на спицу шарик, прикрепленный к центру диска пружиной. Шарик при вращении занимает такое положение на спице, при котором сила натяжения пружины оказывается равной произведению массы шарика на центростремительное ускорение ω ²R (R – расстояние шарика от центра диска).

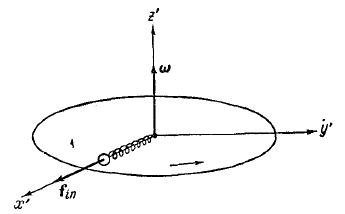
Рис. 16.

Силы инерции во вращающейся системе отсчета

Относительно системы отсчета, связанной с диском, шарик покоится, так как, кроме силы, действующей со стороны пружины, к шарику приложена сила инерции:

f_in = mω2R (46)

направленная вдоль радиуса от центра диска. Силу инерции (46), возникающую во вращающейся (по отношению к инерциальным системам) системе отсчета, на­зывают центробежной силой инерции. Различные точки во вращающейся системе отсчета обладают различным по величине и направлению ускорением по отношению к инерциальной системе. В соответствии с этим центробежная сила инерции зависит от положения тела во вращающейся системе отсчета.

Центробежная сила инерции действует на тело во вращающейся системе отсчета независимо от того, покоится тело в этой системе (как мы предполагали до сих пор) или движется относительно нее со скоростью v'.

При точном решении задач о движении тел относительно земной поверхности нужно учитывать центробежную силу инерции, равную тω_з²Rз* cosφ, где т — масса тела, ω₃ — угловая скорость вращения Земли вокруг ее оси, R₃ —радиус земного шара, φ — широта местности.