2015-02-27
561
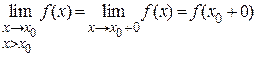
| - называется правосторонним пределом функции f (x) в точке  или пределом справа. 
|
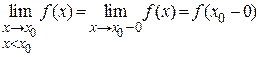
| - называется левосторонним пределом функции f (x) в точке или пределом слева.
|
Теорема 1.1. Для того, чтобы существовал предел функции 
, необходимо и достаточно чтобы существовали односторонние пределы функции равные между собой, т. е.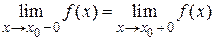 
Д о к а з а т е л ь с т в о.
Необходимость. Пусть существует предел . Тогда для любого e > 0 существует окрестность 
такая, что " х Î значение
f (x) Î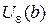 
независимо от того стремится х к слева (x < ) или справа (x > ). Следовательно, существуют и односторонние пределы.
Достаточность. Пусть существуют равные между собой односторонние пределы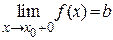 
и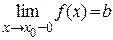 
. Тогда в случае 
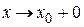для любого e > 0 существует окрестность 
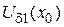такая, что " x> Î 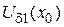значение f (x) Î 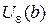. Также в случае 
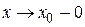для того же e > 0 существует окрестность 
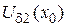такая, что " x < Î 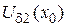значение f (x) Î 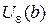. Тогда для заданного значения e > 0 при 
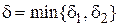, " х Î значение функции f (x) Î 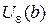независимо от того x > или x < , т. е. предел существует.
|
|
|
