Пусть имеется функция 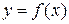 с областью определения D и множеством значений Е. Пусть существует точка
с областью определения D и множеством значений Е. Пусть существует точка  , являющаяся предельной для множества D.
, являющаяся предельной для множества D.
Говорят, что х стремится к  , если можно в области D выбрать бесконечное число различных последовательностей
, если можно в области D выбрать бесконечное число различных последовательностей 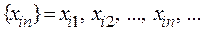 i Î N стремящихся к
i Î N стремящихся к  .
.
Пусть любой последовательности значений независимой переменной 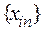 , стремящейся к
, стремящейся к  , соответствует последовательность
, соответствует последовательность 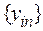 значений функции
значений функции 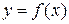 (
(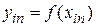 ), стремящаяся к некоторому значению
), стремящаяся к некоторому значению 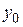 . Тогда говорят о пределе функции.
. Тогда говорят о пределе функции.
Определение предела функции по Гейне. Число b называется пределом функции 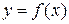 при
при 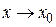 (
(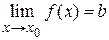 ), если любой последовательности
), если любой последовательности 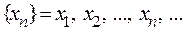 , (
, (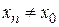 ), стремящейся к
), стремящейся к  , соответствует последовательность значений функции
, соответствует последовательность значений функции 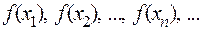 , стремящаяся к b.
, стремящаяся к b.
Определение предела функции по Коши (на языке e-d). Число b называется пределом функции 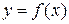 при
при 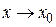 (
(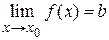 ), если для любого положительного числа e существует такое положительное число d, зависящее от e, что если значение х принадлежит d-окрестности числа
), если для любого положительного числа e существует такое положительное число d, зависящее от e, что если значение х принадлежит d-окрестности числа  , то значение функции
, то значение функции 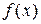 принадлежит e-окрестности числа b.
принадлежит e-окрестности числа b.
Кратко с помощью кванторов можно записать
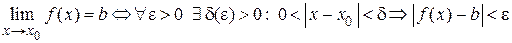 .
.
Пример 1.1. Доказать, что 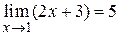 .
.
Используем последнее соотношение из определения предела функции по Коши. Так как 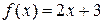 , b = 5, а
, b = 5, а  = 1, то
= 1, то
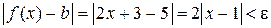 Û
Û 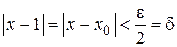 .
.
Отсюда следует, что для любого 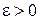 существует
существует 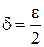 такое, что если
такое, что если 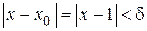 , то
, то 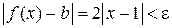 . Это и подтверждает справедливость соотношения
. Это и подтверждает справедливость соотношения 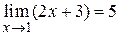 .
.
Аналогично данному примеру докажем еще три предела.
Пример 1.2. Доказать, что 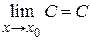 , где С = const.
, где С = const.
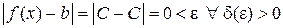 .
.
Пример 1.3. Доказать, что 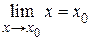 .
.
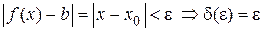 .
.
Пример 1.4. Доказать, что 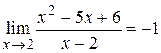 .
.
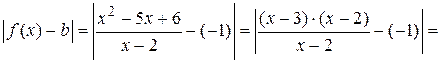
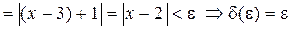 .
.
Для случая, когда 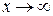 определение предела формулируется следующим образом.
определение предела формулируется следующим образом.
Определение предела функции при 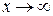 .Число b называется пределом функции
.Число b называется пределом функции 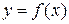 при
при 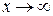 (
(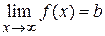 ), если для любого положительного числа e существует такое положительное число N, зависящее от e, что если значение
), если для любого положительного числа e существует такое положительное число N, зависящее от e, что если значение 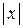 > N, то значение функции
> N, то значение функции 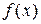 принадлежит e-окрестности числа b (
принадлежит e-окрестности числа b (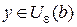 ).
).
Кратко с помощью кванторов можно записать
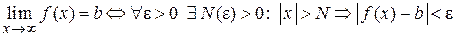 .
.
Аналогично могут быть сформулированы определения предела функции при 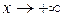 и
и 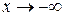 , а именно
, а именно
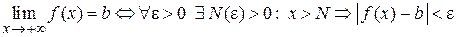 ;
;
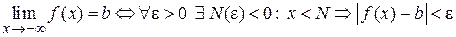 .
.
 2015-02-27
2015-02-27 753
753








