Интегрируя первый раз, получим:
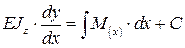
Разделив на жёсткость сечения 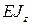 , получим уравнение для углов поворота сечений:
, получим уравнение для углов поворота сечений:
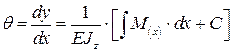 ,
,
где С первая постоянная интегрирования. Определяем из граничных условий:
Для балки с одной точкой опоры (консоль) угол поворота в точке опоры равен нулю:
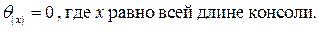
Для балки на двух и более опорах углы поворота в опорах будут принимать максимальные значения. Угол поворота будет равен нулю на границе между участками. Если на эпюре изгибающего момента есть вершина параболы, то можно взять значение х в том месте, где на эпюре изгибающего момента максимум:
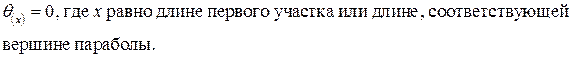
Интегрируя уравнение для углов поворота ещё раз, получим уравнение перемещений (прогибов):
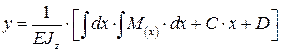 ,
,
где D вторая постоянная интегрирования. Определяем из граничных условий:
Для балки с одной точкой опоры перемещение в точке опоры равно нулю:
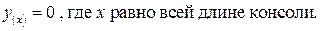
При найденном уже значении С, можно вычислить D. Для балки с одной точкой опоры максимальное перемещение будет на свободном конце (при х=0) и будет равно:
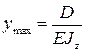 ,
,
где 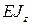 - жесткость сечения при изгибе. Если знак «+», перемещение направлено вверх и совпадает с направлением вверх оси оу. Если знак «-», то перемещение направлено вниз.
- жесткость сечения при изгибе. Если знак «+», перемещение направлено вверх и совпадает с направлением вверх оси оу. Если знак «-», то перемещение направлено вниз.
Мы научились находить перемещение, если участок один.
Граничные условия выбираются в зависимости от конструкции балки.
Для балки с защемлённым концом (консоль) граничные условия будут следующие:
Перемещения и угол поворота сечения будут равны нулю в точке защемления при значении расстояния х, равном длине консоли.
Для балки на двух опорах значения перемещений в точках опоры, при значениях расстояний х, соответствующих точкам опоры, равняются нулю.
Таким способом вычисляют значение перемещения, если количество участков в конструкции не больше двух. Недостаток в том, что интегрирование каждого участка даёт две постоянные интегрирования.
Если участков два, то неизвестных постоянных интегрирования будет четыре.
К двум граничным условиям (равенства нулю перемещений или углов поворота в определённых точках и при определённом значении длины), указанным выше, нужно добавить ещё два условия: плавности и непрерывности изогнутой линии балки на границе между участками.
Условие плавности – углы поворота сечений на границе участков равны:
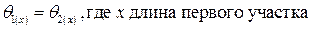 ;
;
Условие непрерывности изогнутой линии – перемещения на границе участков одинаковы:
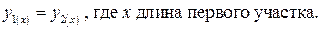
Решить систему из четырёх уравнений, где будет четыре неизвестные постоянные интегрирования, можно определить максимальное значение перемещения.
Пример 1. Определить максимальное перемещение консольной балки, длинной l, если к свободному концу приложена нагрузка Р.
Решение: Запишем приближённое дифференциальное уравнение изогнутой линии:
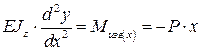 ,
,
Проинтегрируем первый раз, получим:
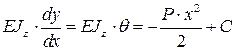 ,
,
Определим значение постоянной интегрирования С из граничных условий – угол поворота в точке опоры при х=l будет равен нулю:
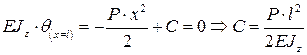 .
.
Интегрируем второй раз для определения перемещения:
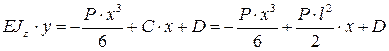 ,
,
Определим значение D из граничных условий – перемещение в точке опоры, при х = l, будет равно нулю:
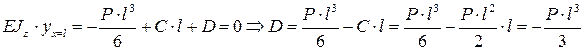 ,
,
После нахождения постоянных интегрирования, определим максимальное перемещение, которое будет на краю балки, при х=0:
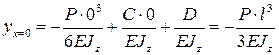 .
.
Определение перемещений методом начальных параметров.
Метод начальных параметров является более удобным для балок с большим количеством участков. Суть метода начальных параметров заключается в выравнивании констант интегрирования по участкам. В результате неизвестными остаются лишь две из них:
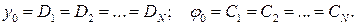
Оставшиеся константы интегрирования имеют простой физический смысл:
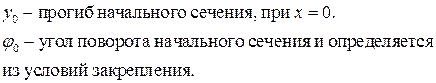
Для произвольной балки постоянного по длине сечения, нагруженной k моментами 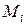 и m сосредоточенными силами
и m сосредоточенными силами 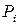 , включая реакции опор, а также n равномерно-распределёнными нагрузками
, включая реакции опор, а также n равномерно-распределёнными нагрузками 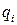 уравнения углов поворота и прогибов записываются одним уравнением сразу для всей балки (для всех участков)
уравнения углов поворота и прогибов записываются одним уравнением сразу для всей балки (для всех участков)
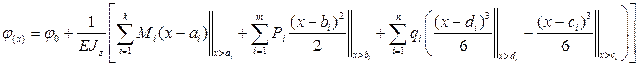
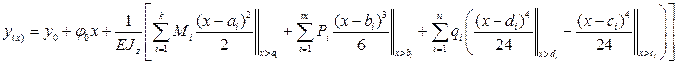
где 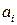 - координата сечения, где приложена i сосредоточенный момент
- координата сечения, где приложена i сосредоточенный момент 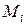 ;
;
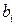 - координата сечения, где приложена i сосредоточенная сила
- координата сечения, где приложена i сосредоточенная сила 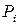 ;
;
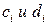 - координаты начала и конца i равномерно - распределённой нагрузки.
- координаты начала и конца i равномерно - распределённой нагрузки.
Двойные чёрточки у каждого из слагаемых показывают, при каком условии данное слагаемое включается в вычисления, а именно при определении прогибов и углов поворота в произвольном сечении с координатой – х. В выше приведённых уравнениях удерживаются только те слагаемые, которые учитывают нагрузки, приложенные к балке левее рассматриваемого сечения.
В уравнениях метода начальных параметров принято следующее правило знаков для внешних нагрузок: 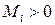 ,если он направлен почасовойстрелке;
,если он направлен почасовойстрелке; 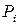 > 0 и
> 0 и 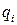 > 0, если они направлены вверх.
> 0, если они направлены вверх.
Пример 2. Определить углы поворота сечений в точках А и В, максимальное перемещение балки, расположенной на двух опорах методом начальных параметров. Длина балки l = а + в. На границе участков приложена нагрузка Р.
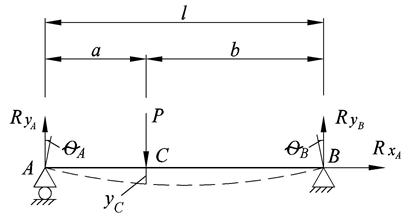
Для определения опорных реакций составляем уравнения равновесия:
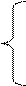
SХi= Rвх = 0
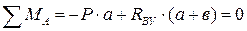
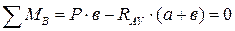
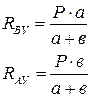
Проверка: SУi= RАУ + RBУ – Р = 0
Для решения применяем метод начальных параметров.
Определяем с помощью граничных условий следующие неизвестные:
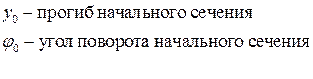
Для балки, расположенной на двух опорах, перемещения в точках А и В равны нулю, поэтому два граничных условия имеют следующий вид:
Перемещения в точках А и В равны нулю.
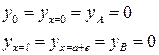
Для определения прогиба начального сечения и угла поворота начального сечения воспользуемся уравнением перемещений и граничными условиями.
Уравнение перемещений для любого сечения:
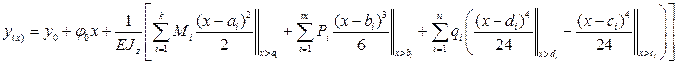 Используя начальные условия:
Используя начальные условия:
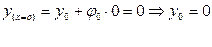
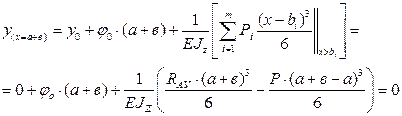
Определяем 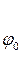 из выше указанного уравнения:
из выше указанного уравнения:
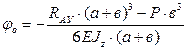
Подставим в уравнение найденное ранее значение 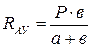 ,
,
учитывая, что l = а + в, после упрощений, получим:
Начальный угол поворота или угол поворота сечения в точке А равен:
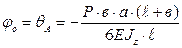
Знак «-» означает поворот угла по часовой стрелке.
Определим перемещение в точке С - 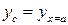
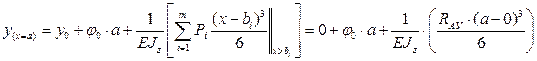
Подставим в уравнение значение 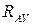 и
и 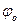 получим:
получим:
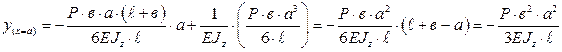
Перемещение в точке С:
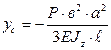
Знак «-» означает перемещение вниз.
Определим угол поворота конечного сечения
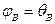
Для этого воспользуемся формулой для угла поворота метода начальных параметров:
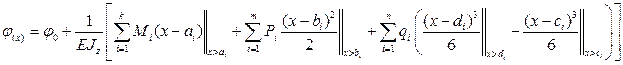
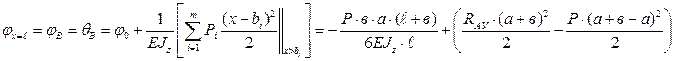
После подстановки значения 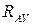 и упрощений, получим:
и упрощений, получим:
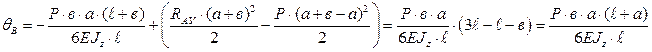
Угол поворота сечения точки В равен:
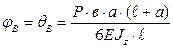
Знак «+» означает поворот угла против часовой стрелки.
 2015-02-27
2015-02-27 3895
3895
