Сложным называется напряжённое состояние при котором на трех взаимно-перпендикулярных площадках действуют нормальные и касательные напряжения.
Напряжение, перпендикулярное площадке называется нормальным и вычисляется по формуле:
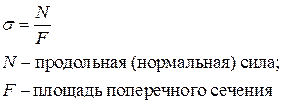
Напряжение, расположенное на площадке, называется касательным и вычисляется по формуле:
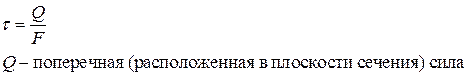
Оказывается при любом сложном напряжённом состоянии тела через каждую его точку можно провести три взаимно-перпендикулярные площадки, где будут отсутствовать касательные напряжения. Только нормальные.
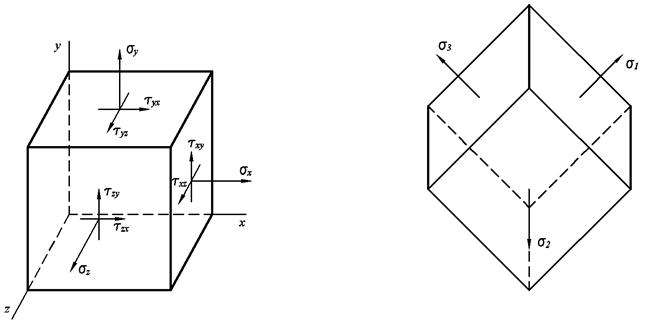
При этом они распределяются следующим образом 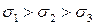 .
.
Например: 200 МПа > 150 МПа > 120 МПа.
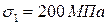 ;
; 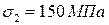 ;
; 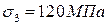 ,
,
С учётом знака:
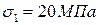 ;
; 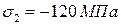 ;
; 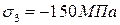
Площадки, на которых действует только один вид напряжений, называются главными.
В зависимости от количества главных напряжений, приложенных к главным площадкам, различают три вида напряжённого состояния в точке:
1. Все 3 главных напряжения не равны нулю. Такое напряжённое состояние называется объёмным (например, подводная лодка под водой).
2. Если одно из главных напряжений равно нулю. Такое напряжённое состояние называется плоским. Например, вал. В этом случае он испытывает сжатие по двум направлениям, при условии, если шкив не вращается. При вращении шкива появится ещё касательное напряжение, действующее на вал.
|
|
|
3. Одно главное напряжение не равно нулю. Такое напряжённое состояние называется линейным. Простое растяжение или сжатие.
В случае сложного напряжённого состояния необходимо привести все действующие напряжения к линейному состоянию и рассматривать сложное напряжённое состояние как простое линейное растяжение или сжатие.
Сначала определим главные напряжения для плоского напряжённого состояния, избавившись от касательных напряжения:
Для этого вырежем у детали элемент. Напряжения 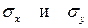 не будут главными, так как действуют ещё и касательные напряжения.
не будут главными, так как действуют ещё и касательные напряжения.
Существуют формулы, позволяющие переходить от не главных напряжений к главным напряжениям:
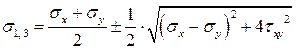
Получили плоское напряжённое состояние.
Для проверки прочности достаточно сравнить наибольшее главное 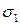 или модуль главного напряжения
или модуль главного напряжения 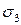 (при отрицательном значении) с допускаемым
(при отрицательном значении) с допускаемым 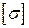 .
.
Если 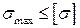 , значит прочность будет обеспечена
, значит прочность будет обеспечена
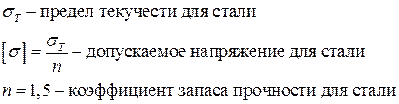
Для хрупких материалов максимальные отрицательные значения сравнивают с допускаемым значением на сжатие, положительные на растяжение. При этом коэффициент запаса прочности п=2.
Рассмотрим вторую обратную задачу:
При известных главных напряжениях нужно найти нормальные и касательные напряжения в любой точке наклонного сечения.
Дано: 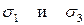 , напряжения действуют по двум взаимно перпендикулярным направлениям - плоское двухосное напряжённое состояние.
, напряжения действуют по двум взаимно перпендикулярным направлениям - плоское двухосное напряжённое состояние.
|
|
|
Найти: 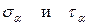 , нормальное и касательное напряжения, действующие в наклонном сечении.
, нормальное и касательное напряжения, действующие в наклонном сечении.
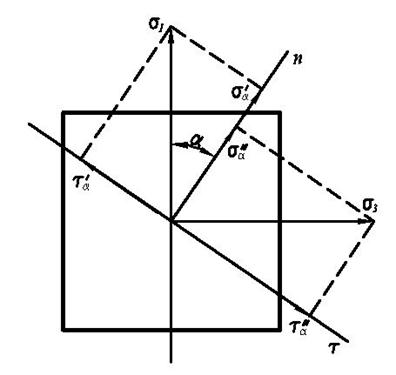
Рассмотрим отдельно действие 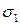
Напряжения в наклонных сечениях от действующего напряжения 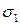 будут равны:
будут равны:
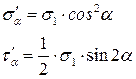
Рассмотрим действие напряжения 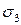 , действующее к наклонному сечению под углом
, действующее к наклонному сечению под углом 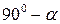
Напряжения в наклонных сечения от действующего напряжения 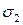 будут равны:
будут равны:
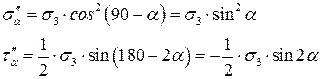
Если сложить все нормальные и касательные напряжения в наклонном сечении, получим полные нормальные и касательные:
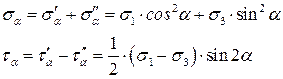
Если в формулу для 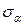 подставить значение
подставить значение 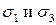 , то при любом значении угла
, то при любом значении угла 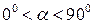 , напряжение в наклонном сечении -
, напряжение в наклонном сечении - 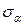 всегда будет меньше
всегда будет меньше 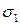 , так как
, так как 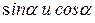 всегда меньше единицы, а в число меньшее единицы в квадрате будет ещё меньше.
всегда меньше единицы, а в число меньшее единицы в квадрате будет ещё меньше.
Это значит, что из всех напряжений главные самые большие.
Рассмотрим случай действия всех главных напряжений 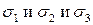 . Объёмное напряженное состояние. Если в направлении действия
. Объёмное напряженное состояние. Если в направлении действия 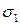 будет происходить растяжение, то в направлении
будет происходить растяжение, то в направлении 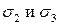 будет происходить сжатие. Можно привести к обобщённому закону Гука.
будет происходить сжатие. Можно привести к обобщённому закону Гука.
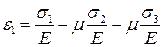
или
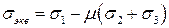 , если
, если
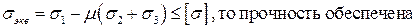
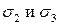 уменьшают действие
уменьшают действие 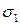 .
.
Аналогично для относительных деформаций 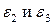 можно записать:
можно записать:
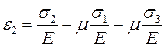
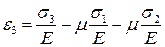
Из всех относительных деформаций 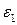 будет самая большая.
будет самая большая.
Если 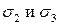 будут действовать внутрь, то будет знак «+».
будут действовать внутрь, то будет знак «+».
 2015-02-27
2015-02-27 8963
8963








