Общий вид:
у¢¢ + а1у¢ + а2у = f(x), (14)
где 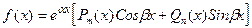 . (15)
. (15)
Здесь Pm(x) и Qn(x) - алгебраические многочлены степеней соответственно m и n.
В этом случае общее решение (14) получается как сумма общего решения (13) и какого-либо частного решения (14): уо. н. = уо. о. + уч. н..
Покажем, как находить уч. н., когда f(х) имеет вид (15). Исходя из конкретного вида (15), составляется число 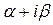 . Далее ставится вопрос: является ли
. Далее ставится вопрос: является ли 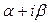 корнем характеристического уравнения (13¢). Здесь возможны 3 случая, для каждого из которых строится уч. н..
корнем характеристического уравнения (13¢). Здесь возможны 3 случая, для каждого из которых строится уч. н..
Объединим эти случаи в табл.2.
Таблица 2.
Число 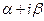
| Вид уч. н. |
| 1. Не является корнем характеристического уравнения | уч. н. = 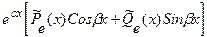
|
| 2. Является корнем характеристического равнения кратности 1 | уч. н . = 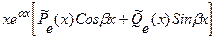
|
| 3. Является корнем характеристического уравнения кратности 2 |  уч. н. = уч. н. = 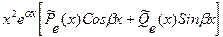
|
Здесь 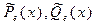 - алгебраические многочлены степени
- алгебраические многочлены степени 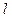 , где
, где 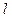 = max(m, n). Коэффициенты
= max(m, n). Коэффициенты 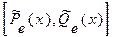 находятся методом неопределенных коэффициентов так, как это показано на следующем примере.
находятся методом неопределенных коэффициентов так, как это показано на следующем примере.
ПРИМЕР. у¢¢ - 4у = х - 1.
Это - неоднородное уравнение 2-го порядка с постоянными коэффициентами и со стандартной правой частью.
Характеристическое уравнение: к2 - 4 = 0. к1 = 2, к2 = -2.
уо. о. = С1e2х + С2e-2х (случай (а) табл.1).
Составляем 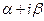 . Т. к. здесь a = 0 и b = 0, то
. Т. к. здесь a = 0 и b = 0, то 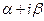 = 0; число 0 не является корнем характеристического уравнения, т. е. Это 1-й случай табл. 2. Следовательно, уч. н. = Ах + В (здесь А и В - неизвестные коэффициенты. Найдем их.). Подставим уч. н. в исходное уравнение. Т. к. у¢ч. н. = А, у¢¢ч. н. = 0, то
= 0; число 0 не является корнем характеристического уравнения, т. е. Это 1-й случай табл. 2. Следовательно, уч. н. = Ах + В (здесь А и В - неизвестные коэффициенты. Найдем их.). Подставим уч. н. в исходное уравнение. Т. к. у¢ч. н. = А, у¢¢ч. н. = 0, то
-4 * (Ах + В) = х - 1.
Приравниваем слева и справа коэффициенты при одинаковых степенях Х (в этом и заключается метод неопределенных коэффициентов).
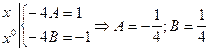 .
.
Итак, уч. н. = 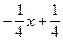 . Тогда уо. н. = уо. о. + уч. н. =
. Тогда уо. н. = уо. о. + уч. н. = 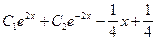 - есть общее решение исходного уравнения.
- есть общее решение исходного уравнения.
 2015-02-04
2015-02-04 414
414








