Второй способ (с помощью собственных значений матрицы Гессе)

Матрица G (х) размерностью(n x n) считается положительно определенной, если все ее собственные значения m₁, m₂,…, m _n положительны, т.е. m _j > 0 для всех j = 1, 2,…, n.

Матрица G (х) считается отрицательно определенной, если собственные значения отрицательны, т.е. m _j < 0 для всех j = 1, 2,…, n.

Если среди собственных значений G встречаются и положительные и отрицательные, то матрица является знакопеременной, а исследуемая функция – невыпуклой.

Для определения собственных значений необходимо решить характеристическое уравнение:

,

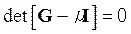где I – квадратная единичная матрица; det – знак определителя.

Матрица 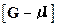отличается от матрицы Гессе тем, что по диагонали располагаются члены вида .

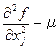Так для двухмерной функции f (x ₁, x ₂)характеристическое уравнение будет иметь вид:

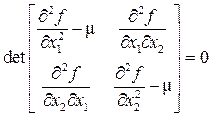(4.10)

Собствееные значения m₁ и m₂есть корни обыкновенного квадратного уравнения m ² + b m + c = 0, образуются после раскрытия определителя.

Для примера возьмем функции двух переменных:

f (x) = 2 – 2 x ₁ –2 x ₂ + x ₁²+ x ₂² – x ₁ x ₂

Координаты экстремальной точки x * определяются решением системы уравнени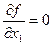й

и 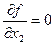равны x ₁* = 2, x ₂* = 2

Гессиан 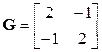. После решения характеристического уравнения 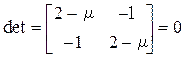, т.е. квадратного уравнения (2 – m)² – 1 = 0 получены собственные значения m₁ = 3, m₂ = 1, т.е. матрица G является положительно определенной. Следовательно, функция f (x) является выпуклой и в экстремальной точке х * = (2,2) принимает минимальное значение f (x *) = –2.

Оба способа проверки достаточных и необходимых условий экстремума второго порядка приведены в табл.4.2.

Пример 4.4. Найти экстремум функции 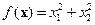на множестве Е ².

Решение. 1. Запишем необходимые условия экстремума первого порядка:

;

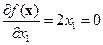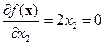
В результате решения системы получаем стационарную точку x * = (0,0).

2. Проверим выполнение достаточных условий экстремума.

Первый способ: Матрица Гессе имеет вид 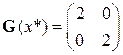.Так как М₁ = 2 > 0,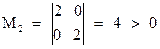 , то в точке x* локальный минимум (строка 1 в табл.4.2).

Второй способ: Найдем собственные значения матрицы Гессе, используя (4.10):

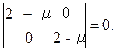Отсюда 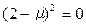и 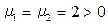. Так как все собственные значения положительны, то в точке x * локальный минимум (строка 1 в табл. 4.2). Из примера 3.3 следует, что функция является строго выпуклой на множестве Е ². Поэтому точка локального минимума является и точкой глобального минимума (согласно п.3, утверждение 3.1).

3. Вычислим значение функции в точке глобального минимума: f (x *) = 0.

Пример 4.5. Найти экстремум функции 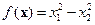на множестве Е².

Решение. 1. Запишем необходимые условия первого порядка:

; .

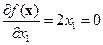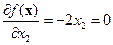В результате решения системы получаем стационарную точку x * = (0,0).

2. Проверим выполнение достаточных условий экстремума и необходимых условий второго порядка.

Первый способ: Матрица Гессе имеет вид 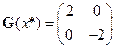. Так как М₁ = 2 > 0, 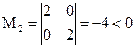, то достаточныое условия экстремума не выполняются (строки 1 и 2 в табл.4.2). Проверим выполнение необходимых условий второго порядка.

Главные миноры первого порядка (m = 1) получаются из M₂ в результате вычеркивания n – m =2 – 1 = 1 строк и столбцов, с одинаковыми номерами: – 2, 2. Главный минор второго порядка (m = 2) получается из M₂ в результате вычеркивания n – m= 0 строк и столбцов, т.е. совпадает с M₂: -4. Отсюда следует, что необходимые условия экстремума второго порядка не выполняются (строки 3 и 4 в табл.4.2). Так как матрица Гессе не является нулевой, то можно сделать вывод о том, что в точке х * нет экстремума (строка 6 в табл.2.1).

Таблица 4.2

Критерий проверки достаточных и необходимых условий второго порядка в задаче поиска безусловного экстремума

№ п/п		G(x *)	Условия	Первый способ	Второй способ	Тип стационарной точки
		>0	Достаточные условия экстремума	M1 > 0, M2 > 0,…, M n > 0	μ1 > 0, μ2 > 0,…,μ n > 0	Локальный минимум
		<0	Достаточные условия экстремума	M1 < 0, M2 > 0, M3 < 0,…, (-1) n M n > 0	μ1 < 0, μ2 < 0,…,μ n > 0	Локальный максимум
		³0	Необходимые условия экстемума второго порядка	Все главные миноры определителя матрицы G(x*) неотрицательны	μ1 ³ 0, μ2 ³ 0,…, μ n ³ 0	Может быть локальный минимум, требуется дополнительное исследование
		£0	Необходимые условия экстемума второго порядка	Все главные миноры четного порядка неотрицательны, а нечетного порядка неположительны	μ1 £ 0, μ2 £ 0,…, μ n £ 0	Может быть локальный максимум, требуется дополнительное исследование
		=0	Необходимые условия экстемума второго порядка	Матрица Гессе состоит из нулевых элементов	μ1 = 0, μ2 = 0,…, μ n = 0	Требуется дополнительное исследование
		>0, <0	Необходимые условия экстемума второго порядка	Не выполняются условия п.1…5	μ n имеют разные знаки	Нет экстремума

Второй способ: Найдем собственные значения матрицы Гессе, используя (4.10):

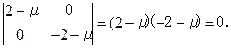
Отсюда m₁ = 2 > 0, m₂ = –2 < 0, т.е. собственные значения имеют разные знаки. Поэтому точка х * не является точкой минимума или максимума (строка 6 в табл.4.2), а является седловой точкой (аналогична изображенной на рис.4.6).

3. Так как экстремум не достигается ни в одной точке, 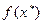не вычисляется.

Пример 4.6 Проверить, является ли выпуклой квадратичная функция

.

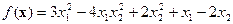Решение. Найдем матрицу Гессе

.

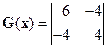Угловые (главные) миноры этой матрицы положительны:

М₁ = 6 > 0, .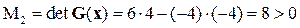

Поэтому, согласно критерию Сильвестра, матрица G (x) положительно определенная, и, следовательно, функция строго выпуклая.