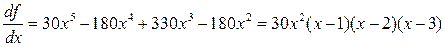Решение. Ясно, что первая производная обращается в нуль в точках х = 0,1,2,3, и, следовательно, эти точки можно классифицировать как стационарные

.

Ясно, что первая производная обращается в нуль в точках х = 0,1,2,3, и, следовательно, эти точки можно классифицировать как стационарные.

.

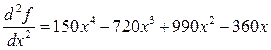Вычислим значения второй производной в четырёх точках х = 0; 1; 2; 3 (табл.4.1).

Таблица 4.1

Значения f (x) и d ² f / d x ²

x	f (x)	d 2 f / d x2
	27,5 5,5	-120

Отсюда следует, что х = 1; 3 – точки локального минимума, а х = 2 – точка локального максимума. Чтобы идентифицировать х = 0, вычислим третью производную.

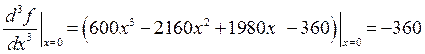
Так как эта производная отлична от нуля и имеет нечётный порядок, то точка х = 0 является не точкой оптиума, а точкой перегиба.

Пример 4.3. Максимизировать 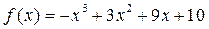на интервале –2 £ х £ 4.

Решение. Имеем

.

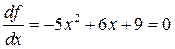Решая это уравнение, получим две стационарные точки х = 3 и х = - 1, которые расположены внутри заданного интервала. Для того, чтобы найти глобальный максимум, вычислим значения функции в точках х = 3, -1, -2, 4.

¦(3) = 37, ¦(-2) = 12, ¦(-1) = 5, ¦(4) = 30.

Таким образом, точка х = 3 соответствует максимальному значению функции ¦ на интервале [-2, 4]. Для проверки выполнения достаточных условий экстремума и необходимых условий второго порядка используются два способа.