f (x) = x 14+ x 24- x 12-2 x 1 x 2- x 22 →extr.
Решение. Запишем необходимое условие экстремума I порядка:
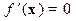
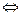
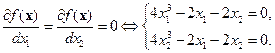
Решая эту систему уравнений, находим стационарные точки x 1=(x 1, x 2) = (1,1), х 2 = (-1,-1), х 3 = (0,0). Для проверки условий второго порядка выписываем матрицу вторых производных:
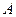 =
= 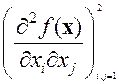 =
= 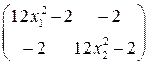
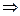
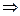
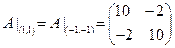 ,
, 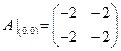 .
.
Матрица 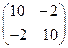 по критерию Сильвестра положительно определена. По достаточному условию локального экстремума функции нескольких переменных точки (1,1) и (-1,-1) доставляют локальный минимум функции f.
по критерию Сильвестра положительно определена. По достаточному условию локального экстремума функции нескольких переменных точки (1,1) и (-1,-1) доставляют локальный минимум функции f.
Поскольку 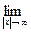 f (x)=
f (x)= 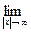
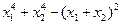 =+
=+ 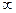 , то по следствию из теоремы Вейерштрасса она достигает своего абсолютного минимума. Следовательно, (1,1), (-1,-1)
, то по следствию из теоремы Вейерштрасса она достигает своего абсолютного минимума. Следовательно, (1,1), (-1,-1) 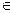 absmin, S min = f (1,1) = f (-1,-1) = -2.
absmin, S min = f (1,1) = f (-1,-1) = -2.
Матрица 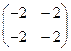 по критерию Сильвестра не является ни положительно, ни отрицательно определенной. Она является неположительно определенной матрицей (А ≤ 0) и не является неотрицательно определенной матрицей (A < 0). Следовательно, не выполняется необходимое условие локального минимума. Поэтому х 3 = (0,0)
по критерию Сильвестра не является ни положительно, ни отрицательно определенной. Она является неположительно определенной матрицей (А ≤ 0) и не является неотрицательно определенной матрицей (A < 0). Следовательно, не выполняется необходимое условие локального минимума. Поэтому х 3 = (0,0) 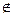 locmin f. Поскольку
locmin f. Поскольку
f (h,- h) = 2 h 4 > 0 = f (x 3)
при малых h ≠0, то х 3 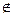 locmax f. Очевидно, что f max = +
locmax f. Очевидно, что f max = + 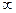 .
.
 2015-02-04
2015-02-04 767
767








