627
В теории оптимизации иногда более удобно рассматривать общую задачу оптимизации, в которой понятие решение определяется таким образом, что оно всегда существует. Для того чтобы сформулировать эту обобщённую задачу, понадобится определение точной нижней грани.
Число (или символ – ¥)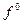 
называют точной нижней гранью или инфимумомфункции ¦ на множестве X, если неравенство 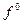£ ¦ (x) имеет место для всех хÎХ и, кроме того, для любого числа ¦’> 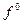найдётся точка х’ÎХ такая, что верно неравенство ¦(x’)<¦’. Тот факт, что 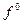– точная нижняя грань функции ¦ на множестве Х, записывают в виде
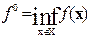(4.8)
Аналогично вводится понятие точной верхней грани. Число (или символ +¥)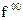 
называютточной верхней гранью или супремумом функции ¦ на множестве Х, если неравенство f 00³¦ (x) справедливо для всех хÎХ и для любого числа ¦’ < f 00найдётся точка х’ÎХ такая, что верно неравенство ¦(x’) >¦’. Для точной верхней грани используется обозначение
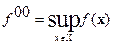
Как указано выше, не всегда можно указать точку, в которой точная грань достигается, т.е. точку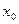 
, для которой 
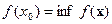. Поэтому в обобщённой задаче минимизации 
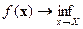под решением понимают не отдельную точку, как это имеет место в обычной задаче оптимизации, а последовательность точек 
, 
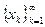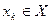, k =1,2,…,такую, что
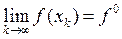(4.9)
Эта последовательность всегда существует и называется, минимизирующей последовательностью.
Таким образом, обобщённая задача минимизации целевой функции ¦ на множестве Х заключается в отыскании числа (или символа -¥) 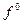и последовательности точек 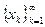, , 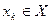k = 1,2,…, таких, что выполняются равенства (4.8) ... (4.9).
